Cinte's Leetcode Record
0%

287. Find the Duplicate Number

Posted on Edited on In Disqus:
Symbols count in article: 1.6k Reading time ≈ 1 mins.

287. Find the Duplicate Number

很绕，由于不能改数组，这种情况废弃

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int lo = 0, hi = nums.size() - 1;
        while(lo < hi)
        {
            int mid = (lo + hi) / 2;
            if(mid + 1 <= nums[mid]) // 这里不能用不等号，因为只如果全是正确排列的话，这个一定是等号，如果mid左边出现了重复，那么mid的数会不等于mid+1，但是nums[mid] < mid + 1的情况当且仅当重复数出现在左边或本身就是重复数时才会发生。因此这种情况必然是hi=mid。而nums[mid] >= mid + 1时，如果自身是重复数，那么其余的重复数必然出现在他的右边，因为如果在左边的话，那肯定就小于了。如果自身不是，那就是nums[mid] == mid + 1的情况，也肯定在右边。
                lo = mid + 1;
            else if(mid + 1 > nums[mid])
                hi = mid;
        }
        return hi;
    }
};

T(N) : O(nlogn)

S(n) : O(1)

另一种使用二分

设cnt为数组中小于等于当前元素的元素的个数，设当前mid为target

将重复的数字看作是插入到了数组中，当插入到了比target小的数中，那么设i < target，cnt[i]必然<i，当插入到了比target大的数中，设j > target，cnt[j]必然>j，因为多了一个比他小的cnt。

如果都正常的话，在1~target-1区间中的数cnt[i]==i，target~n中的数必然>j

由此，在1~n区间内进行二分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int cnt = 0;
        int lo = 1, hi = nums.size() - 1;
        while(lo < hi)
        {
            int mid = lo + (hi - lo) / 2;
            cnt = 0;
            for(auto& num : nums)
                cnt += num <= mid ? 1 : 0;
            if(cnt <= mid)
                lo = mid + 1;
            else
                hi = mid;
        }
        return hi;
    }
};
使用cycle，有点静态链表的思想，其中的链表组成如图
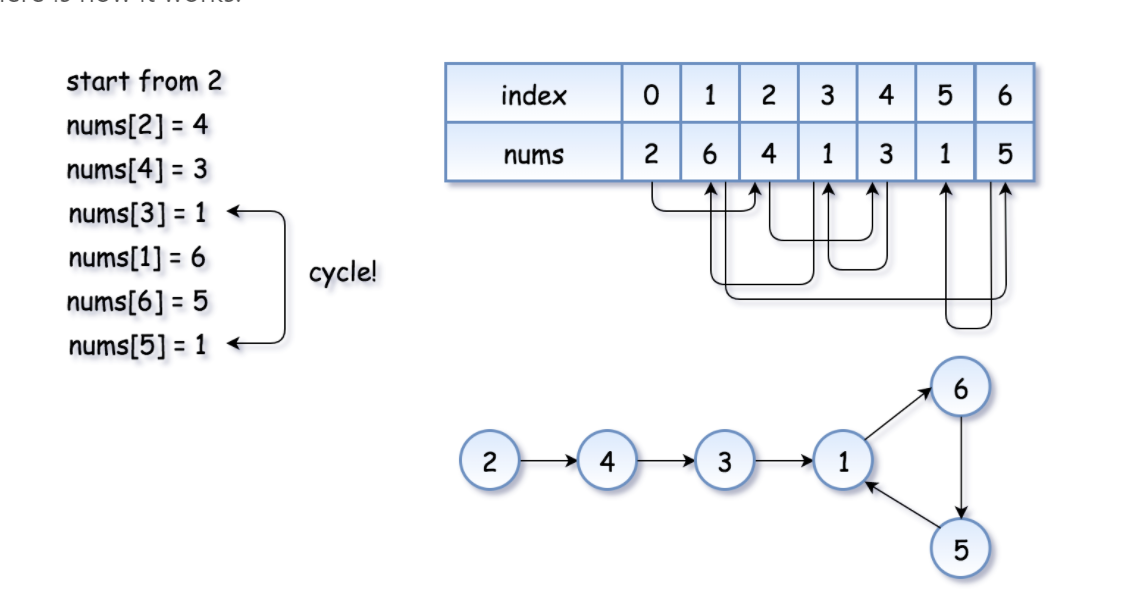image.png

由于位于0处的数字不可能是0，所以他不可能原地跳不出去。 如果碰到一个原地跳不出去的，那就说明已经是环了

最后套用142. Linked List Cycle II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int walker = nums[0];
        int runner = nums[0];
        
        do
        {
            walker = nums[walker];
            runner = nums[nums[runner]];
        }while(walker != runner);
        
        walker = nums[0];
        while(walker != runner)
        {
            walker = nums[walker];
            runner = nums[runner];
        }
        return runner;
    }
};