Brute Force
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
int maxLen = 0;
int curLen = 1;
bool stop = false;
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; ++j)
{
if(matrix[i][j] == '1')
{
while(curLen + i < m && curLen + j < n && !stop)
{
for(int k = j; k <= curLen + j; ++k)
{
if(matrix[i + curLen][k] == '0')
{
stop = true;
break;
}
}
for(int k = i; k <= curLen + i; ++k)
{
if(matrix[k][j + curLen] == '0')
{
stop = true;
break;
}
}
if(!stop)
++curLen;
}
maxLen = max(curLen, maxLen);
curLen = 1;
stop = false;
}
}
}
return maxLen * maxLen;
}
};
|
对于每个大小每次增长，遍历行
DP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int maxLen = 0;
vector<int> dp(matrix[0].size() + 1, 0);
int prev = 0;
for(int i = 1; i <= matrix.size(); ++i)
{
for(int j = 1; j <= matrix[0].size(); ++j)
{
int tmp = dp[j];
if(matrix[i - 1][j - 1] == '1')
{
dp[j] = min(min(dp[j - 1], dp[j]), prev) + 1;
maxLen = max(dp[j], maxLen);
}else
{
dp[j] = 0;
}
prev = tmp;
}
}
return maxLen * maxLen;
}
};
|
在答案的approach2中，不能使用原矩阵做为dp的矩阵，因为对于char来说，过大的矩阵会使其溢出
approach3还是不咋懂总体是每行扫描更新当前行的值，然后进入下一行后，只需要用到上一行的数据和当前行
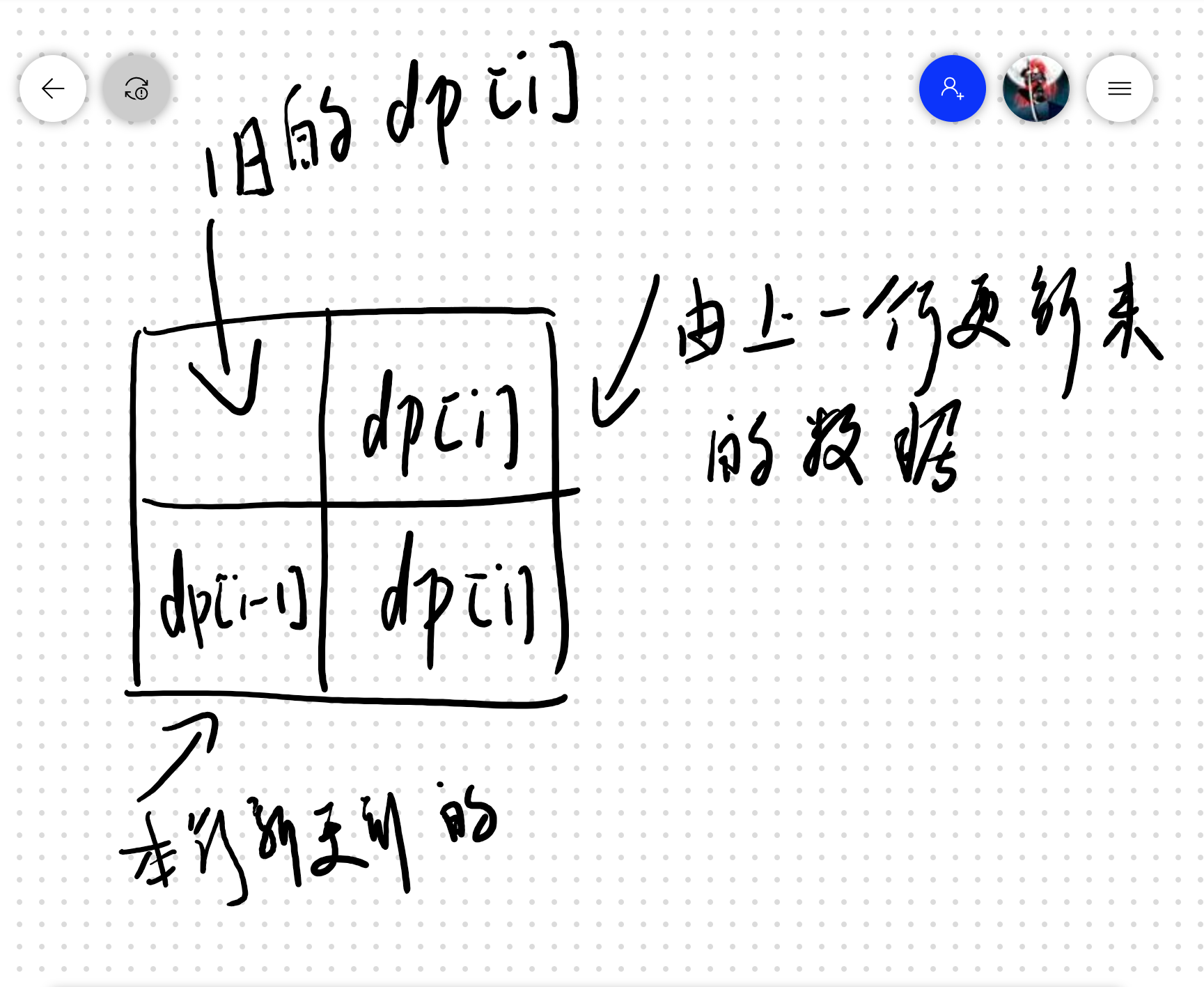image.png