若求是否存在两个子序列相等,只需要求序列中是否存在子序列和等于总序列的一半。所以当和为奇数时候就是无效的。
转化为dp
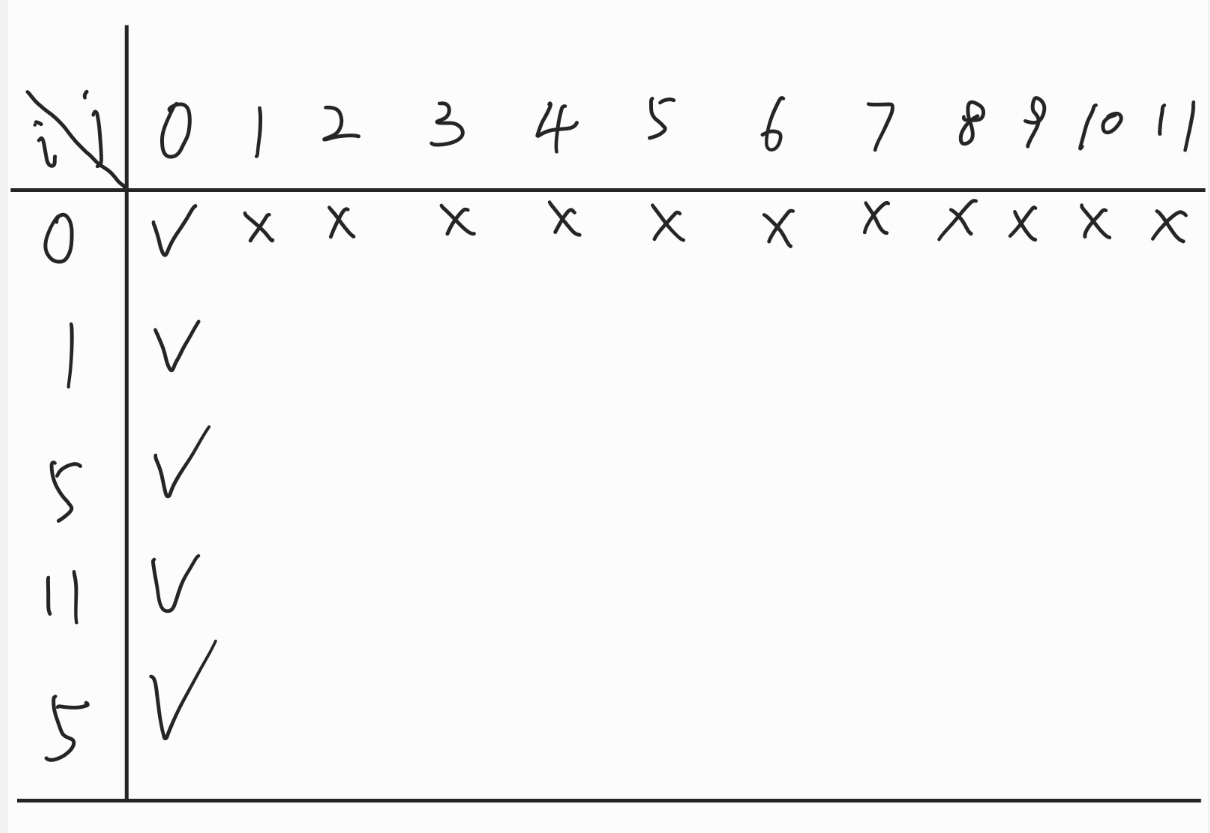
dp[i][j]表示0~i的数字能否获得和为j,若能为true,不能为false。
对于一行的dp[i][j]来说
- 取当前这个
nums[i],则如果0~i-1的数字可以达到j - nums[i]和的话就是true,反之为false。也就是dp[i - 1][j - nums[i]]是否为true
- 不取当前这个
nums[i - 1],则如果0~i-1可以达到和为j,也就是dp[i - 1][j]是否为true。
基础情况是当没有数字时,当且仅当j为0时为true。当和为0时,对于所有数字都是true,因此只需要不取。
二维dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for(auto& num : nums)
sum += num;
if(sum & 1)
return false;
sum >>= 1;
vector<vector<bool>> dp(nums.size() + 1, vector<bool>(sum + 1, false));
dp[0][0] = true;
for(int i = 1; i <= sum; ++i)
dp[0][i] = false;
for(int i = 1; i <= nums.size(); ++i)
dp[i][0] = true;
for(int i = 1; i <= nums.size(); ++i)
{
for(int j = 1; j <= sum; ++j)
{
dp[i][j] = dp[i - 1][j] || (j >= nums[i - 1] ? dp[i - 1][j - nums[i - 1]] : false);
}
}
return dp.back()[sum];
}
};
|
dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for(auto& num : nums)
sum += num;
if(sum & 1)
return false;
sum >>= 1;
vector<bool> dp(sum + 1, false);
dp[0] = true;
for(int i = 1; i <= nums.size(); ++i)
{
for(int j = sum; j > 0; --j)
{
dp[j] = dp[j] || (j >= nums[i - 1] ? dp[j - nums[i - 1]] : false);
}
}
return dp.back();
}
};
|
此处从sum走是因为,i - num是一个小于 i 的值,可以保证走在后面的时候这个值还是上一行生成的结果,如果从小到大走,走到后面时就会把前面的结果刷新掉了
review
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public:
bool canPartition(vector<int>& nums) {
auto sum = accumulate(nums.begin(), nums.end(), 0);
if(sum & 1)
return false;
sum /= 2;
int m = nums.size();
vector<bool> dp(sum + 1, false);
dp[0] = true;
for(int i = 0; i < m; ++i)
{
for(int j = sum; j >= 0; --j)
dp[j] = dp[j] || (j >= nums[i] && dp[j - nums[i]]);
if(dp[sum])
return true;
}
return false;
}
};
|
