1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> heap;
for(auto& num : nums)
{
auto i = std::lower_bound(heap.begin(), heap.end(), num);
if(i == heap.end())
heap.push_back(num);
else
*i = num;
}
return heap.size();
}
};
|
不使用std::lower_bound
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> heap;
for(auto& num : nums)
{
auto i = binarySearch(heap.begin(), heap.end(), num);
if(i == heap.end())
heap.push_back(num);
else
*i = num;
}
return heap.size();
}
private:
vector<int>::iterator binarySearch(vector<int>::iterator begin, vector<int>::iterator end, int num)
{
vector<int>::iterator it;
int count = end - begin;
int step;
while(count > 0)
{
it = begin;
step = count / 2;
it += step;
if(*it < num)
{
begin = ++it;
count -= step + 1;
}else
count = step;
}
return begin;
}
};
|
review
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> piles;
for(auto& num : nums)
{
auto i = binarySearch(piles, 0, piles.size(), num);
if(i != piles.size())
piles[i] = num;
else
piles.push_back(num);
}
return piles.size();
}
private:
int binarySearch(vector<int>& nums, int lo, int hi, int target)
{
while(lo < hi)
{
int mid = (lo + hi) >> 1;
if(nums[mid] < target)
lo = mid + 1;
else
hi = mid;
}
return hi;
}
};
|
视频介绍:
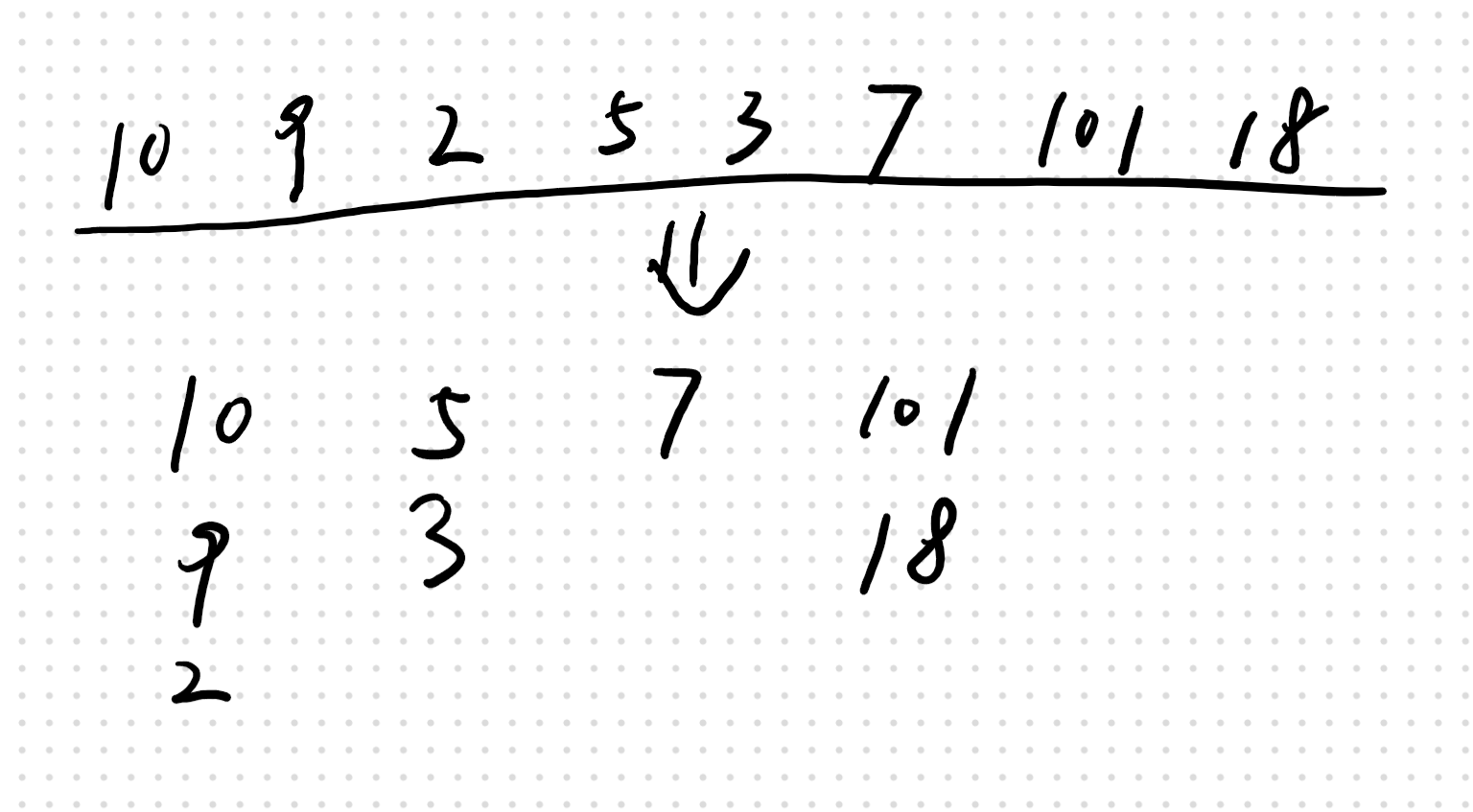 如图,把所有牌分堆,从左开始寻找,一旦找到他比某个牌堆的顶端少,就放过去,以贪婪原则。
如图,把所有牌分堆,从左开始寻找,一旦找到他比某个牌堆的顶端少,就放过去,以贪婪原则。
这样分出的排队数量就是里面的最长增长的串,保证这一点可以通过数学归纳法,详情见视频3:43, 直观的理解是因为:
每个排队中的顺序都是依据原数组中顺序递减的,因此,每个牌堆中最多只能取一张牌,因此增长序列长度<=牌堆数
dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
vector<int> f(n);
int ret{ 0 };
for(int i = 0; i < n; ++i)
{
int len = 1;
for(int j = 0; j < i; ++j)
if(nums[i] > nums[j])
len = max(len, f[j] + 1);
ret = max(len, ret);
f[i] = len;
}
return ret;
}
};
|
引368. 最大整除子集
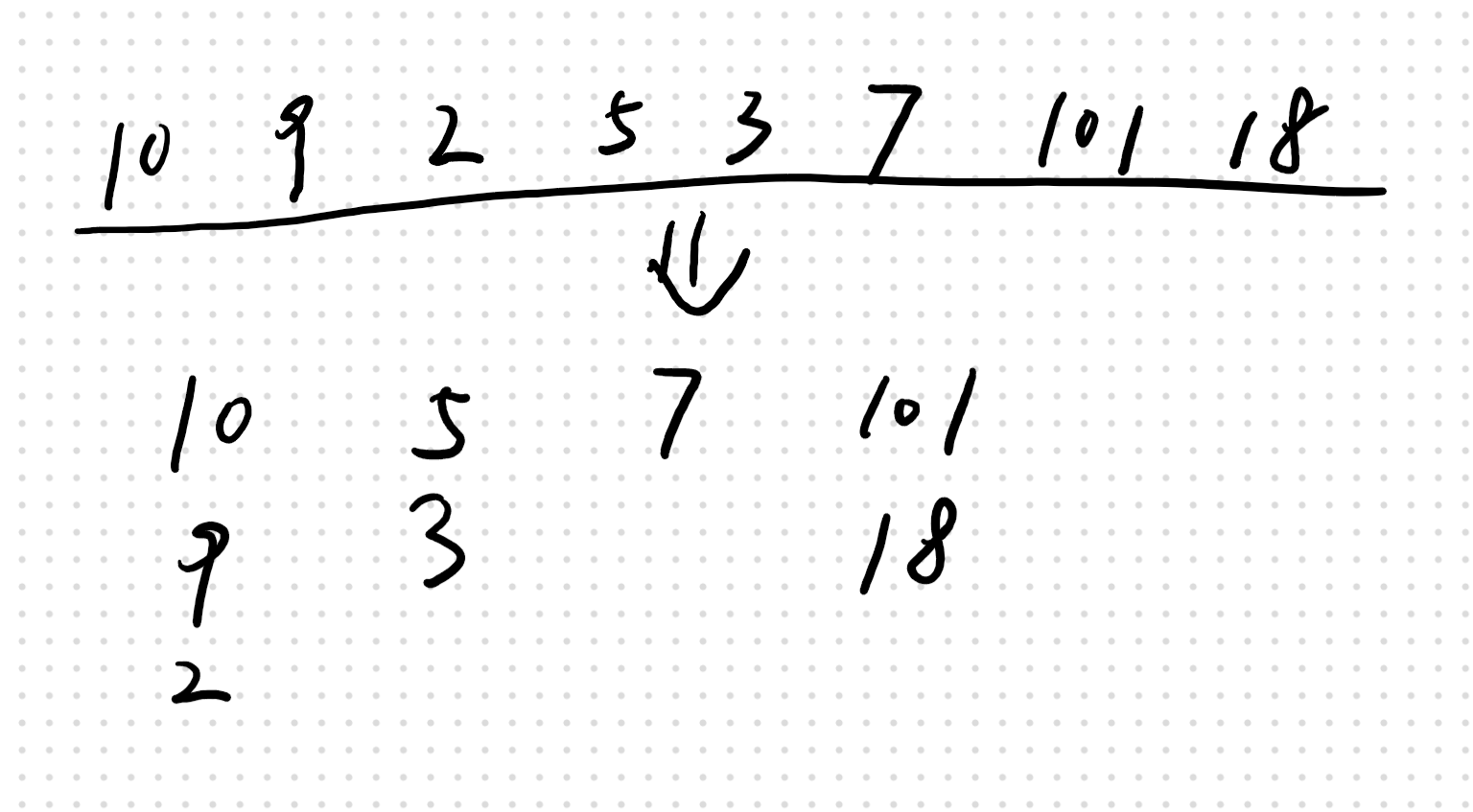 如图,把所有牌分堆,从左开始寻找,一旦找到他比某个牌堆的顶端少,就放过去,以贪婪原则。
如图,把所有牌分堆,从左开始寻找,一旦找到他比某个牌堆的顶端少,就放过去,以贪婪原则。