1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution {public : int trap (vector <int >& height) if (height.empty()) return 0 ; vector <int > leftWater (height.size() + 1 ) int maxNum = 0 ; int maxIndex = 0 ; for (int i = 0 ; i < height.size(); ++i) { if (height[i] > maxNum) { maxIndex = i; maxNum = height[i]; } leftWater[i + 1 ] = maxNum - height[i] + leftWater[i]; } maxNum = 0 ; for (int i = height.size() - 1 ; i > maxIndex; --i) { if (height[i] > maxNum) { maxNum = height[i]; } leftWater[maxIndex + 1 ] += maxNum - height[i]; } return leftWater[maxIndex + 1 ]; } };
答案中的dp
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : int trap (vector <int >& height) if (height.empty()) return 0 ; vector <int > left (height.size()) left[0 ] = height[0 ]; vector <int > right (height.size()) right[height.size() - 1 ] = height.back(); for (int i = 1 ; i < height.size(); ++i) left[i] = max(left[i - 1 ], height[i]); for (int i = height.size() - 2 ; i >= 0 ; --i) right[i] = max(right[i + 1 ], height[i]); int ans = 0 ; for (int i = 0 ; i < height.size(); ++i) ans += min(left[i], right[i]) - height[i]; return ans; } };
借图
使用stack
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution {public : int trap (vector <int >& height) if (height.empty()) return 0 ; stack <int > bars; int cur = 0 ; int res = 0 ; while (cur < height.size()) { while (!bars.empty() && height[cur] > height[bars.top()]) { auto top = bars.top(); bars.pop(); if (bars.empty()) break ; int distance = cur - bars.top() - 1 ; int heightBounded = min(height[cur], height[bars.top()]) - height[top]; res += distance * heightBounded; } bars.push(cur++); } return res; } };
每碰到一个比之前的障碍高的就计算一次体积,每次计算的是方形,进行填充,由于比较低的在填完后被pop,而他的障碍会被push,因此在填充完毕后,对于后面来看,这就是一条水平线,示意图如下
Two Points
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution {public : int trap (vector <int >& height) int left = 0 ; int right = height.size() - 1 ; int leftMax = 0 ; int rightMax = 0 ; int res = 0 ; while (left < right) { if (height[left] < height[right]) { if (leftMax < height[left]) leftMax = height[left]; res += leftMax - height[left]; ++left; }else { if (rightMax < height[right]) rightMax = height[right]; res += rightMax - height[right]; --right; } } return res; } };
中间盛的水可以由左右边界来决定,当左边比右边矮的时候,水由左边边界决定,因为条件决定了左边不会比右边高,所以左边的水量又会受左边的最高峰影响,左边最高峰之左,水由边界决定,最高峰之右,由最高峰决定。将其最高峰之左再细分,又会有许多局部最高峰,由此一来,对于每一步更新其最高峰,更新最高峰之前的水由前一个局部边界决定,更新最高峰后的水由最高峰决定,同时这个局部最高峰又成了下一个区域的边界。
复习
dp
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : int trap (vector <int >& height) int n = height.size(); vector <int > memo (n) int before = 0 ; for (int i = 0 ; i < n; ++i) memo[i] = before = max(before, height[i]); int ret = 0 ; int right = 0 ; for (int i = n - 1 ; i >= 0 ; --i) { right = max(height[i], right); ret += min(memo[i], right) - height[i]; } return ret; } };
双指针
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : int trap (vector <int >& height) int left = 0 , right = 0 ; int ret = 0 ; int i = 0 , j = height.size() - 1 ; while (i < j) { left = max(left, height[i]); right = max(right, height[j]); if (left < right) ret += left - height[i++]; else ret += right - height[j--]; } return ret; } };
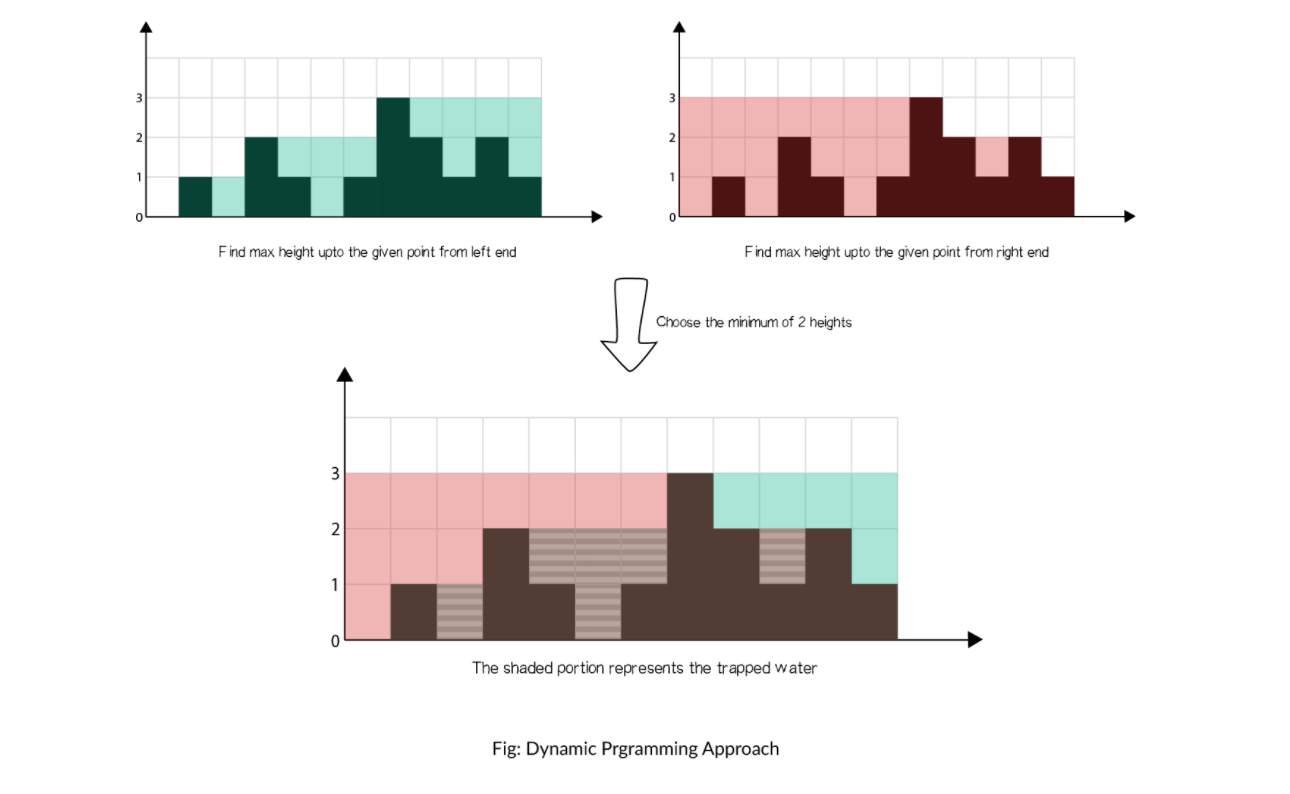 只可意会,左边由两边都是取得最低的量
只可意会,左边由两边都是取得最低的量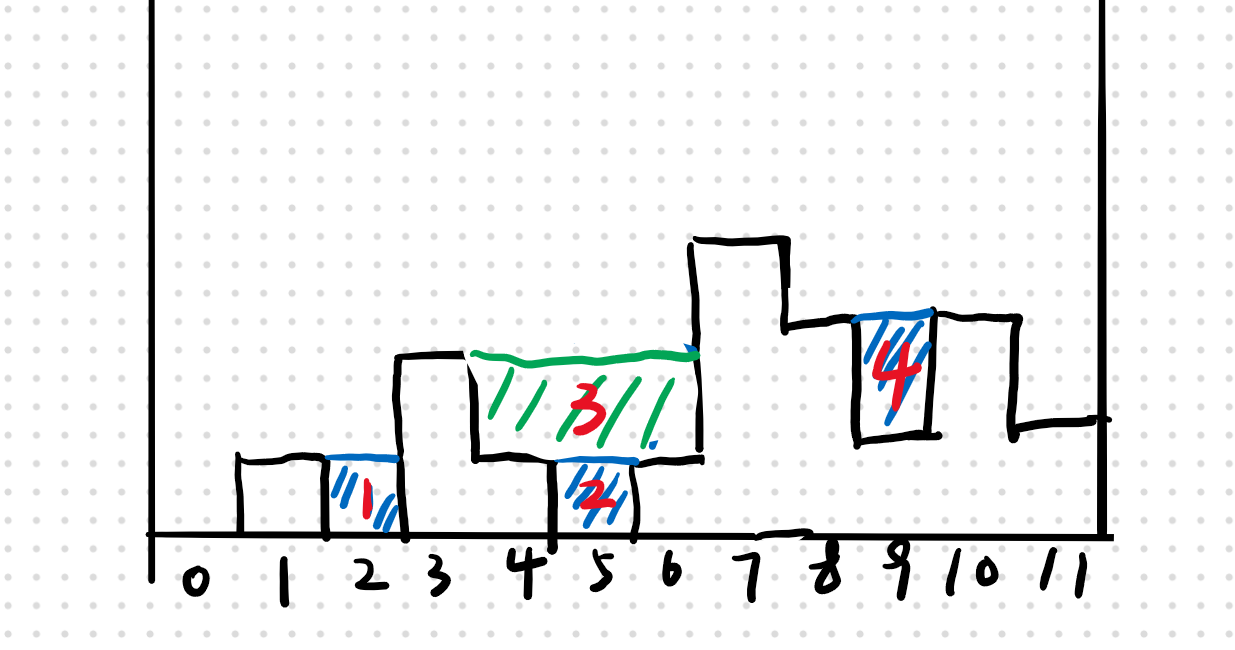 图中红色标号表示填充水块的次序
图中红色标号表示填充水块的次序