128. Longest Consecutive Sequence

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        if(nums.empty())
            return 0;
        sort(nums.begin(), nums.end());
        int ret = 1;
        int tmp = 1;
        for(int i = 1; i < nums.size(); ++i)
        {
            if(nums[i] != nums[i - 1])
            {
                if(nums[i] == nums[i - 1] + 1)
                    ++tmp;
                else
                {
                    ret = max(ret, tmp);
                    tmp = 1;
                }
            }
        }
        return max(ret, tmp);
    }
};

T(n) : O(nlogn)
S(n) : O(1)

排序后，跳过相同的，计算多个子串，如果不相等，就从头开始计算

hash

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        if(nums.empty())
            return 0;
        unordered_set<int> set;
        for(auto& num : nums)
        {
            set.insert(num);
        }
        int ret = 1;
        for(auto& num : nums)
        {
            if(set.find(num - 1) == set.end())
            {
                int tmp = 1;
                int curNum = num + 1;
                while(set.find(curNum) != set.end())
                {
                    ++curNum;
                    ++tmp;
                }
                ret = max(ret, tmp);
            }
            
        }
        return ret;
    }
};

用哈希记录每个值，然后找，而且仅仅从连续子串的开头开始，跳过所有的中间量

明明是O(n)为啥比第一个O(nlogn)还慢

discussion

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_map<int, int> map;
        int r = 0;
        for(auto& num : nums)
        {
            if(!map[num]) // 仅仅对于没建立过路径的数字来建立，因为如果重复建立，会导致结果重复累加
            // 这里的num如果是中间的点的话，更新他不会有什么影响，因为这表示他周围的点已经计算完他们本身为起点或终点的最大长度了，不会重复计算
            // 如果是端点，那也可以更新，总之就是让他不为0。
            // 事实上，这里的map[num]赋值仅仅是为了标记他已经走过，赋任何值都可以
                r = max(r, map[num] = map[num + map[num + 1]] = map[num - map[num - 1]] = map[num - 1] + map[num + 1] + 1); 
        }
        return r;
    }
};

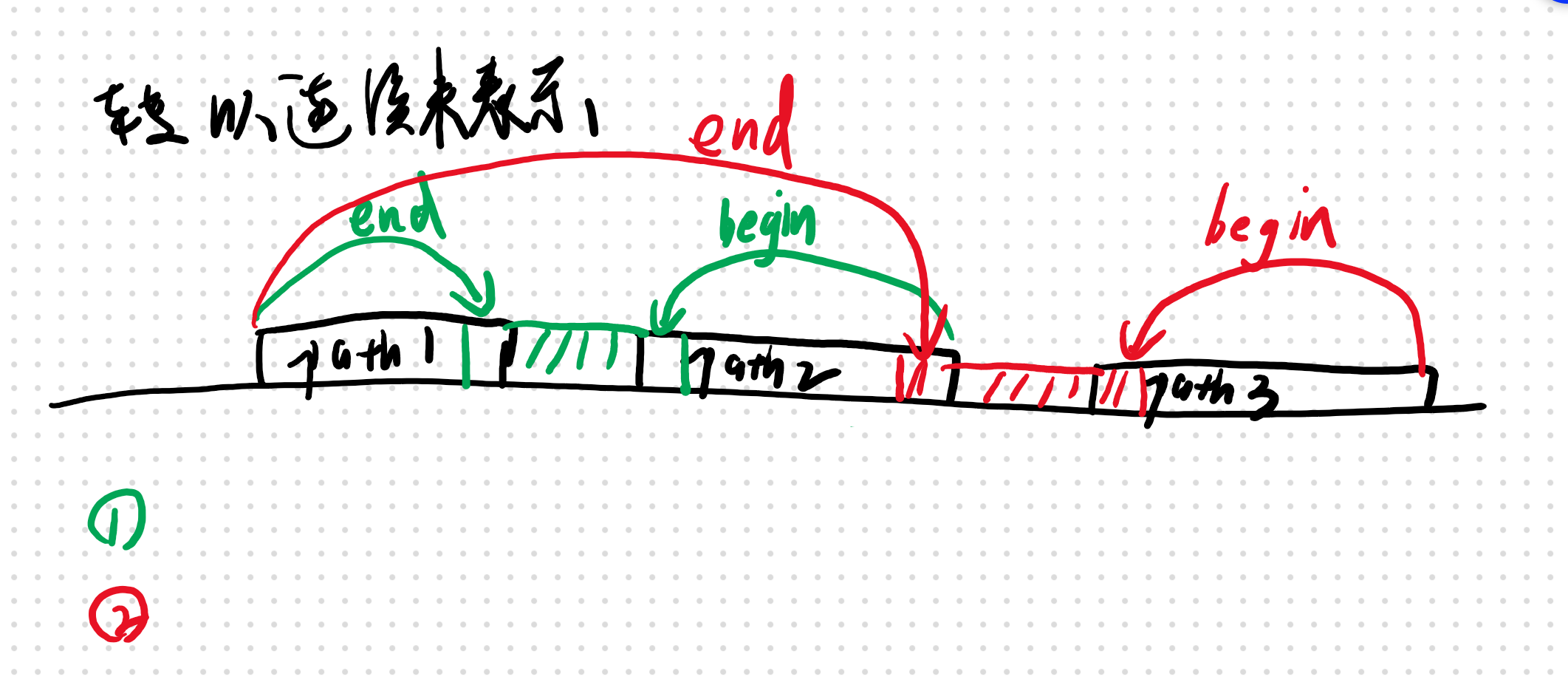
对于n，几种情况

有一条到n-1的路径，则总长度为len(n-1)+1
有一条n+1到后面的路径，则总长度为len(n+1)+1
都没有，则长度为1

对于一条路径来说，比如123456，则对于这条路径的开头和结尾来说，他们的最长长度应该是一样的，给他们赋予同样的值，中间的点会走到，然后会更新值，走过的点就不走了

差不多就是每走到一个点，如果他周围还没有，那就建立一条小路，后面走到中间的后，自然会连接两条小路

对于每个点来说，他都记录以他为起点或者终点的最长路的长度，如果走到的这个点没走到过，那就说明他前面的那条路没有经过现在，必然是反向，于是这个点连接前后，更新始终的值。就仿佛2个水珠的中间滴入一滴水，三者融为一体。