太难理解了！！！！！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
if(matrix.empty())
return 0;
int maxA = 0;
int n = matrix[0].size();
vector<int> left(n, 0);
vector<int> right(n, n);
vector<int> height(n, 0);
for(int i = 0; i < matrix.size(); ++i)
{
int curL = 0, curR = n;
for(int j = n - 1; j >= 0; --j)
{
if(matrix[i][j] == '1')
right[j] = min(right[j], curR);
else
{
right[j] = n;
curR = j;
}
}
for(int j = 0; j < n; ++j)
{
if(matrix[i][j] == '1')
{
++height[j];
left[j] = max(curL, left[j]);
}else
{
height[j] = 0;
left[j] = 0;
curL = j + 1;
}
maxA = max(maxA, (right[j] - left[j]) * height[j]);
}
}
return maxA;
}
};
|
所有信息会进行传递
出现如下这种时[1][4]元素左界会有上面那个来界定，高度也会随之更新，但不必担心由此扰乱更大的矩形的判断，因为这个元素处curR为5，若这个竖着的矩形不是最大矩形，那么这个右界限会保持住传给他的左边隔壁，如果他左边隔壁也不要这个右界限，说明左边隔壁也继承了上一层的信息。那么继续传递过去，如果都不要，那么2是有2层的，不要也无所谓了，肯定比一层长。同理左界限也会传递。由此这一层中的每个元素都会记录他本身所在的矩形，并且是所有局部最大矩形。 还是有点绕
明天去画个图
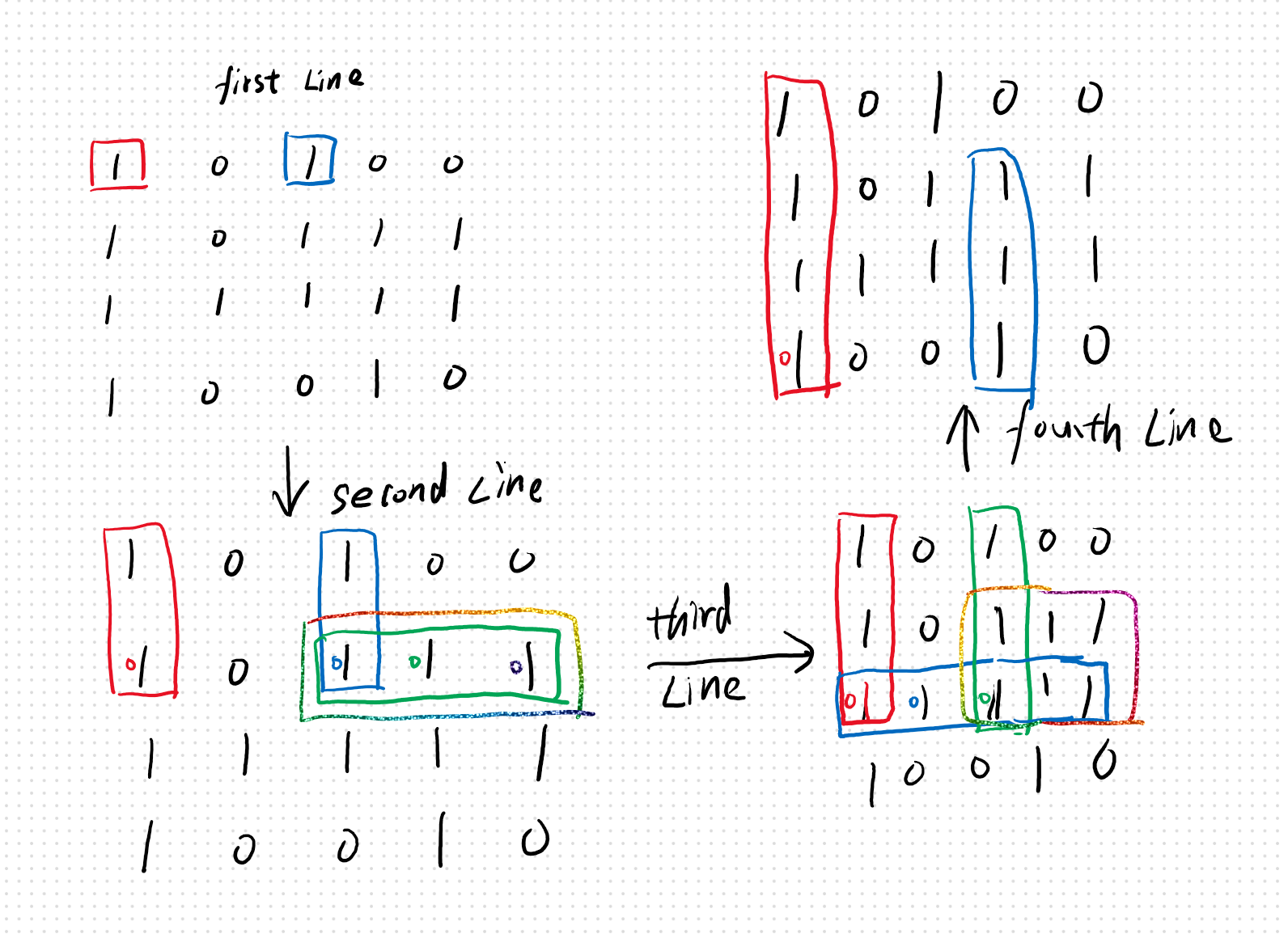1620472343565.png
1
2
3
4
| 1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
|