Cinte's Leetcode Record
0%

剑指 Offer 33. 二叉搜索树的后序遍历序列

Posted on Edited on In Disqus:
Symbols count in article: 1.7k Reading time ≈ 2 mins.

剑指 Offer 33. 二叉搜索树的后序遍历序列

D&Q
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    bool verifyPostorder(vector<int>& postorder) {
        return verify(postorder, 0, postorder.size() - 1);
    }
private:
    bool verify(vector<int>& nums, int i, int j)
    {
        if(i >= j)
            return true;
        int p = i;
        // 此处无需p<j这个条件，因为nums[j]==nums[j]，所以必定不会导致越界
        while(nums[p] < nums[j]) ++p;
        int m = p;
        while(nums[p] > nums[j]) ++p;
        return p == j && (verify(nums, i, m - 1) && verify(nums, m, j - 1));
    }
};

对于一个序列，根在最右边，然后左边的左半边是左子树，右半边是右子树，他们的分界就是左子树全小于根，右子树全大于根，所以只需要通过一个个判断，就可以判断出其中的左子树和右子树，再对子树递归就可以判断了

单调栈+倒序

真的难，还是没想透为什么不管升序要管降序

因为要找大于当前节点中最小的来做parent，所以使用单增栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    bool verifyPostorder(vector<int>& postorder) {
        stack<int> s;
        int parent = INT_MAX;
        for(int i = postorder.size() - 1; i >= 0; --i)
        {
            // 如果升序，压栈，倒序，那么这个节点肯定是某个节点的左节点
            while(!s.empty() && postorder[i] < s.top()) // 因为栈是递增的，所以找到一个刚刚好大于他本身的节点就是他的父亲节点。
            {
                parent = s.top();
                s.pop();
            }
            if(postorder[i] > parent)  
            // 注意这个parent只有在遇到递减数列时候才会赋值，那么有几种情况。
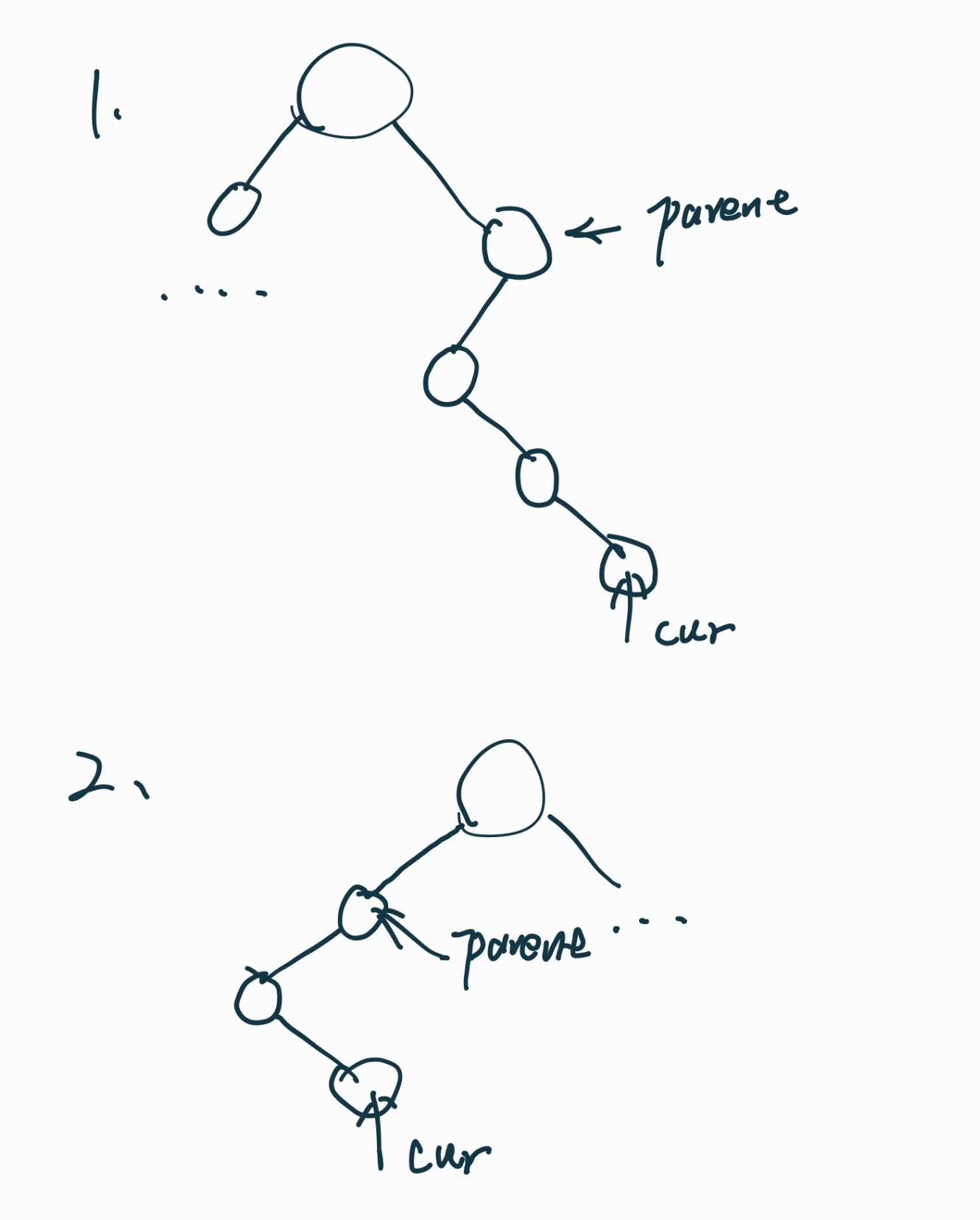
            1. 当当前节点是左子节点，那么parent是这个左子节点的父亲，由上面栈的关系必定可以保证。
            2. 当当前节点是右子节点，那么parent具有几种情况(在倒序情况下是根-右-左)
                1、parent是某个左子节点的父亲，那么他必定大于节点 
                2、往回走，栈逐渐压入，那么parent成为当前节点所在树的某个祖先节点，并且由后序遍历的顺序，这个树肯定在parent的左边。依旧必定大于节点
                return false;
            s.push(postorder[i]);
        }
        return true;
    }
};

SmartSelect_20220706-103930_Samsung Notes.jpg 题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool verifyPostorder(vector<int>& postorder) {
        stack<int> s;
        s.push(INT_MIN);
        int parent = INT_MAX;
        for(int i = postorder.size() - 1; i >= 0; --i)
        {
            while(postorder[i] < s.top())
            {
                parent = s.top();
                s.pop();
            }
            if(postorder[i] > parent)
                return false;
            s.push(postorder[i]);
        }
        return true;
    }
};