Cinte's Leetcode Record
0%

Posted on Edited on In Disqus:
Symbols count in article: 572 Reading time ≈ 1 mins.

[179. 最大数](https://leetcode-cn.com/problems/largest-number/)

类似剑指 Offer 45. 把数组排成最小的数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    string largestNumber(vector<int>& nums) {
        // 自定义排序，对于两个数a,b，他们组合起来时如果ab>ba，那么a就要放在b前面
        sort(nums.begin(), nums.end(), [](int a, int b)
        {
            long sa = 10;
            long sb = 10;
            while(sa <= a)
            {
                sa *= 10;
            }
            while(sb <= b)
            {
                sb *= 10;
            }
            return sa * b + a < sb * a + b;
        });
        // 针对数组中全是0的情况，例如[0,0]，如果不做这个处理会返回"00"
        if(nums[0] == 0)
            return "0";
        string ret;
        for(auto& num : nums)
            ret += to_string(num);
        return ret;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1k Reading time ≈ 1 mins.

162. 寻找峰值

同852. 山脉数组的峰顶索引

同剑指 Offer II 069. 山峰数组的顶部

O(n)时间复杂度，简单的遍历

当全都升序的时候。只有最后一个元素是山峰。没有符合nums[i] > nums[i + 1]的

当全都降序的时候。第一个元素是山峰，直接返回。第一个元素符合nums[i] > nums[i + 1]，后面的符合但是不是解，但是由于已经直接返回了，所以不会影响结果。

当中间有转折的时候。nums[i] > nums[i + 1]必定是符合的。

存不存在符合nums[i] > nums[i + 1]但是不是山峰的情况呢？只在全都降序时候第一个元素之后的存在。而这种情况上面说了对结果没有影响。总而言之就是只需要判断nums[i] > nums[i + 1]就可以了。

1
2
3
4
5
6
7
8
9
class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        for(int i = 0, sz = nums.size(); i < sz - 1; ++i)
            if(nums[i] > nums[i + 1])
                return i;
        return nums.size() - 1;
    }
};
O(logn)二分查找

当nums[mid] > nums[mid + 1]时

这时候他处于一个递减子序列中，那么他的左边必定存在一个山峰，即使左边全是递减的，那么结果也会是左边的第一个元素。

如果他处于一个递增子序列，那么山峰一定会在他的右边。

如果恰好是lo和hi中间一块为单调，但lo和hi又不等于开头和结尾。

假设中间一块单调增加，如果之前的hi要到现在的hi，必定在那里存在一个山峰。

如果中间一块单调减少，如果之前的lo要到现在的lo，必定也在那里存在一个山峰。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int lo = 0, hi = nums.size() - 1;
        while(lo < hi)
        {
            int mid = lo + (hi - lo) / 2;
            // mid总是像左边靠，所以不会存在mid+1越界的情况，当只有一个元素时候，循环已经退出。
            if(nums[mid] > nums[mid + 1])
                hi = mid;
            else
                lo = mid + 1;
        }
        return hi;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 925 Reading time ≈ 1 mins.

150. 逆波兰表达式求值

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。 逆波兰表达式主要有以下两个优点：

去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中。

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/evaluate-reverse-polish-notation 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<int> s;
        for(auto& token : tokens)
        {
            if(token != "+" && token != "-" && token != "*" && token != "/")
                s.push(stoi(token));
            else
            {
                int num2 = s.top();
                s.pop();
                int num1 = s.top();
                s.pop();
                switch(token[0])
                {
                    case '+':
                        s.push(num1 + num2);
                        break;
                    case '-':
                        s.push(num1 - num2);
                        break;
                    case '*':
                        s.push(num1 * num2);
                        break;
                    case '/':
                        s.push(num1 / num2);
                }
            }
        }
        return s.top();
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 900 Reading time ≈ 1 mins.

134. 加油站

根据答案意思，对于[x, y]，区间，如果从x起步无法到达y之后的一个，则所有x和y区间内部的点起步都无法到达y的后一个点。但内部任意起点可以到达y和y之前加油站由此可以避开许多的起始点判定。

证明:

符合上述条件的区间中存在这样的关系 \[ \sum_{i=x}^{y}gas[i] < \sum_{i=x}^{y}cost[i]\newline \sum_{i=x}^{j}gas[i] >= \sum_{i=x}^{j}cost[i]\ j \in [x, j) \newline \] 第一个式子表明无法到达加油站y的下一个加油站，第二个式子表明从x出发可以到达 y以及y之前的所有加油站。

则对于区间中任意节点z \[ \sum_{i=z}^{y}gas[i]\newline = \sum_{i=x}^{y}gas[i] - \sum_{i=x}^{z - 1}gas[i]\newline < \sum_{i=x}^{y}cost[i] - \sum_{i=x}^{z - 1}gas[i]\newline < \sum_{i=x}^{y}cost[i] - \sum_{i=x}^{z - 1}cost[i]\newline = \sum_{i=z}^{y}cost[i] \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int n = gas.size();
        int i = 0;
        while(i < n)
        {
            int gasLeft = 0;
            int cnt = 0;
            while(cnt < n)
            {
                int j = (i + cnt) % n;
                gasLeft += gas[j];
                gasLeft -= cost[j];
                if(gasLeft < 0)
                    break;
                ++cnt;
            }
            if(cnt == n)
                return i;
            else
                i += cnt + 1;
        }
        return -1;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 4.8k Reading time ≈ 4 mins.

127. 单词接龙

近似暴力的BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        int sz = wordList.size();
        vector<int> visited(sz, 0);
        int wordLength = wordList[0].size();
        vector<string> candidates{ beginWord };
        int ret = 1;
        while(!candidates.empty())
        {
            ++ret;
            vector<string> tmp;
            for(auto& cand : candidates)
            {
                for(int j = 0; j < sz; ++j)
                {
                    if(visited[j])
                        continue;
                    auto word = wordList[j];
                    int diff = 0;
                    for(int i = 0; i < wordLength; ++i)
                    {
                        if(word[i] != cand[i])
                            ++diff;
                    }
                    if(diff == 1)
                    {
                        tmp.push_back(word);
                        if(word == endWord)
                            return ret;
                        visited[j] = 1;
                    }
                }
            }
            candidates = tmp;
        }
        return 0;
    }
};
BFS+虚拟节点
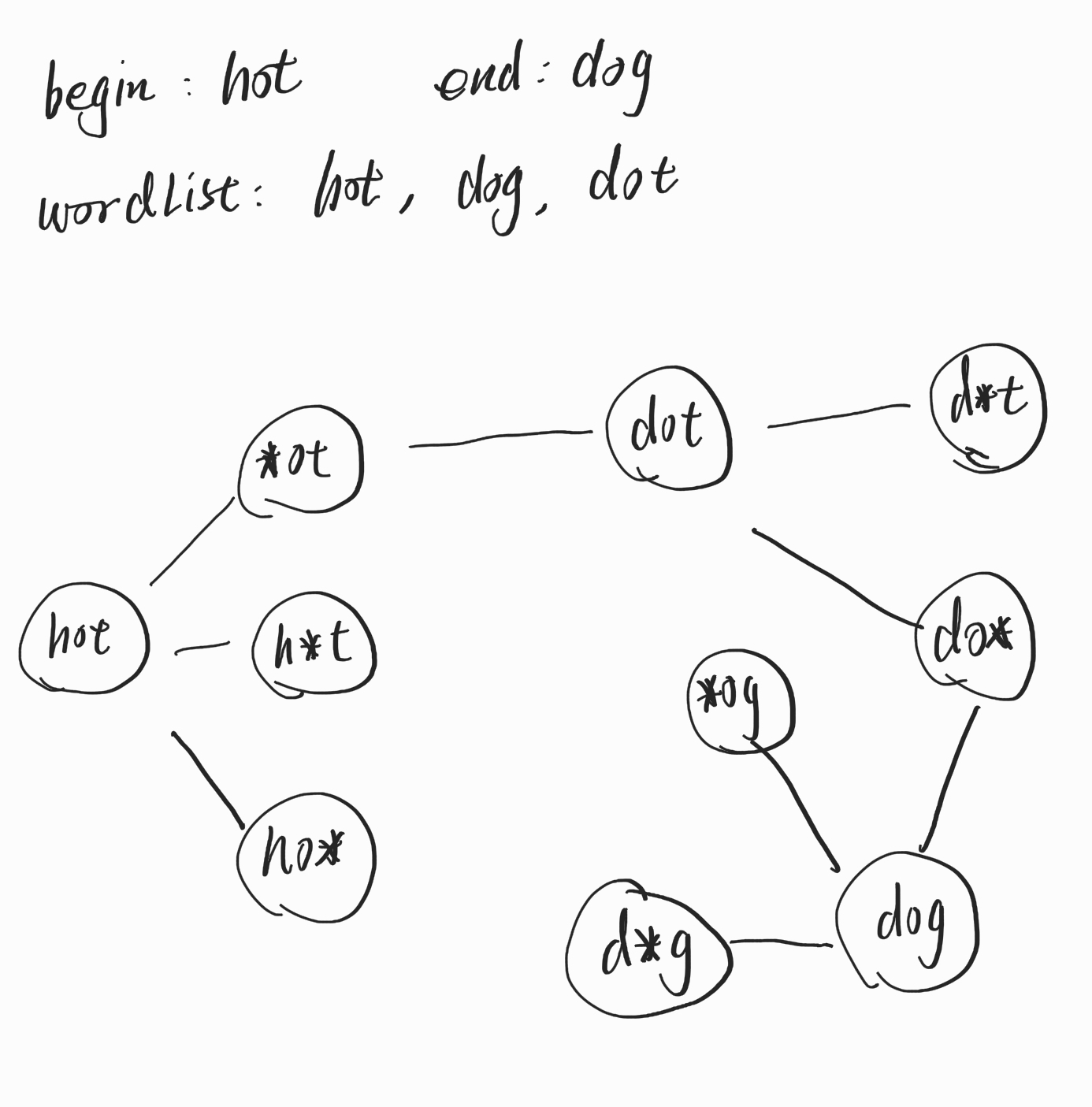
1631071640321.jpg 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        int ret = 0;
        for(auto& word : wordList)
            addEdge(word);
        addEdge(beginWord);
        if(!map.count(endWord)) // 使用count而不是find，参考《Effective STL》第45条
            return 0;
        queue<int> q;
        int endId = map[endWord];
        q.push(map[beginWord]);
        int step = 1; // 因为这种写法中是在if的内部判断是不是邻居点为终点，所以需要设置为什么，不然就少走了一步
        vector<int> visited(nodeNum, 0);
        while(!q.empty())
        {
            ++step;
            for(int i = 0, sz = q.size(); i < sz; ++i)
            {
                auto p = q.front();
                q.pop();
                if(visited[p])
                    continue;
                visited[p] = 1;
                for(auto neighbor : graph[p])
                {
                    if(neighbor == endId)
                        return step / 2 + 1;
                    q.push(neighbor);
                }
            }
        }
        return 0;
    }
private:
    int nodeNum = 0;
    vector<vector<int>> graph;
    unordered_map<string, int> map;
    void addWord(string& s)
    {
        if(!map.count(s))
        {
            map.insert({s, nodeNum++});
            graph.emplace_back();
        }
    }
    void addEdge(string& s)
    {
        addWord(s);
        int id1 = map[s];
        for(auto& ch : s)
        {
            auto tmp = ch;
            ch = '*';
            addWord(s);
            int id2 = map[s];
            graph[id1].push_back(id2);
            graph[id2].push_back(id1);
            ch = tmp;
        }
    }
};

写法二

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        int ret = 0;
        for(auto& word : wordList)
            addEdge(word);
        addEdge(beginWord);
        if(!map.count(endWord))
            return 0;
        queue<int> q;
        int endId = map[endWord];
        q.push(map[beginWord]);
        vector<int> dis(nodeNum, INT_MAX); // 记录步长，顺便记录已经走过的点
        dis[map[beginWord]] = 0;
        while(!q.empty())
        {
            auto p = q.front();
            q.pop();
            if(neighbor == endId)
                return dis[neighbor] / 2 + 1; // 走过的路径长是之前的两倍，而且由于没有计算头节点，所以需要+1
            for(auto neighbor : graph[p])
            {
                if(dis[neighbor] == INT_MAX)
                {
                    dis[neighbor] = dis[p] + 1;
                    q.push(neighbor);
                }
            }
        }
        return 0;
    }
private:
    int nodeNum = 0;
    vector<vector<int>> graph;
    unordered_map<string, int> map;
    void addWord(string& s)
    {
        if(!map.count(s))
        {
            map.insert({s, nodeNum++});
            graph.emplace_back();
        }
    }
    void addEdge(string& s)
    {
        addWord(s);
        int id1 = map[s];
        for(auto& ch : s)
        {
            auto tmp = ch;
            ch = '*';
            addWord(s);
            int id2 = map[s];
            graph[id1].push_back(id2);
            graph[id2].push_back(id1);
            ch = tmp;
        }
    }
};
BFS双向搜索

从begin和end同时开始，如果他们相遇了就是结果，这样可以减少许多分叉的占用

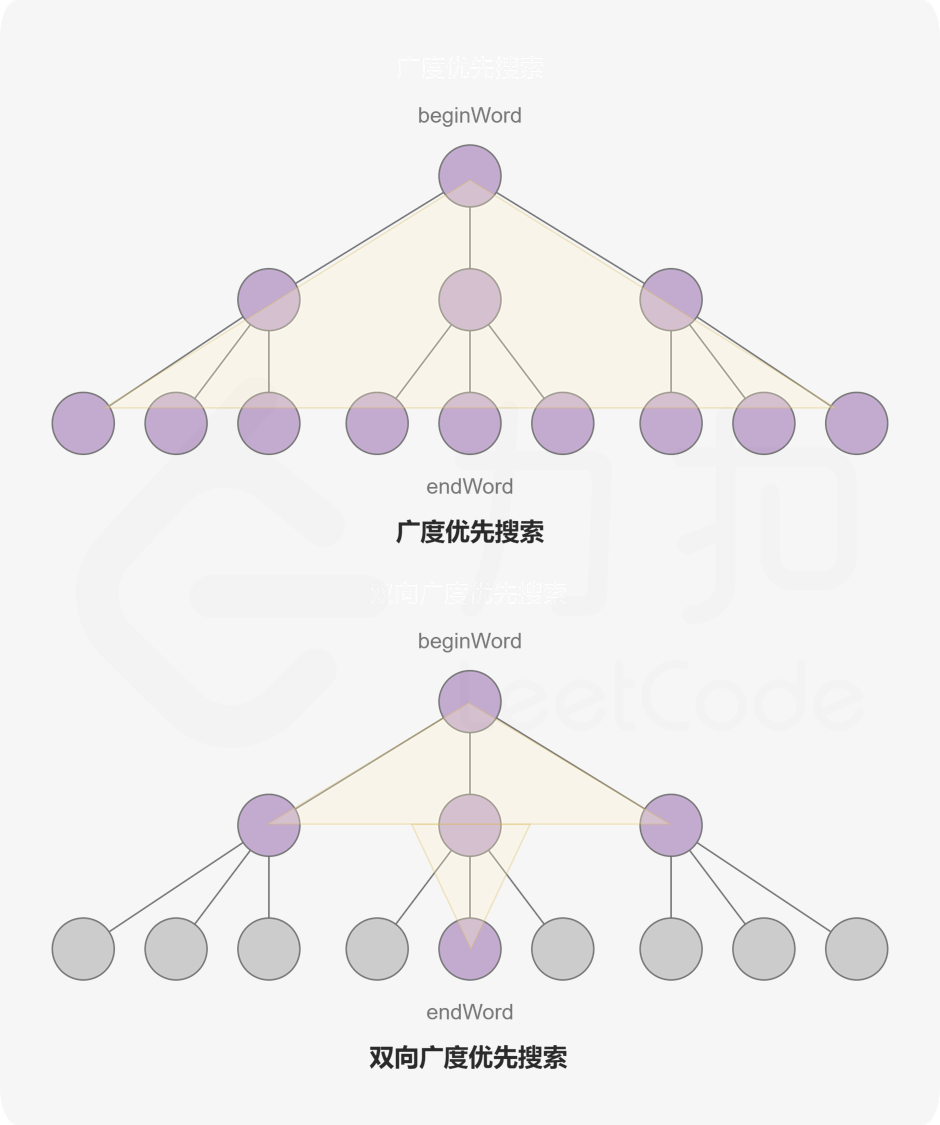
1631086368533.png 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        int ret = 0;
        for(auto& word : wordList)
            addEdge(word);
        addEdge(beginWord);
        if(!map.count(endWord))
            return 0;
        queue<int> qBegin;
        queue<int> qEnd;
        int endId = map[endWord];
        int beginId = map[beginWord];
        qBegin.push(beginId);
        qEnd.push(endId);
        vector<int> disBegin(nodeNum, INT_MAX);
        vector<int> disEnd(nodeNum, INT_MAX);
        disBegin[beginId] = 0;
        disEnd[endId] = 0;
        while(!qBegin.empty() && !qEnd.empty())
        {
            for(int i = 0, sz = qBegin.size(); i < sz; ++i)
            {
                auto p = qBegin.front();
                qBegin.pop();
                if(disEnd[p] != INT_MAX)
                    return (disEnd[p] + disBegin[p]) / 2 + 1;
                for(auto num : graph[p])
                {
                    if(disBegin[num] == INT_MAX)
                    {
                        disBegin[num] = disBegin[p] + 1;
                        qBegin.push(num);
                    }
                }
            }
            for(int i = 0, sz = qEnd.size(); i < sz; ++i)
            {
                auto p = qEnd.front();
                qEnd.pop();
                if(disBegin[p] != INT_MAX)
                    return (disEnd[p] + disBegin[p]) / 2 + 1;
                for(auto num : graph[p])
                {
                    if(disEnd[num] == INT_MAX)
                    {
                        disEnd[num] = disEnd[p] + 1;
                        qEnd.push(num);
                    }
                }
            }  
        }
        return 0;
    }
private:
    int nodeNum = 0;
    vector<vector<int>> graph;
    unordered_map<string, int> map;
    void addWord(string& s)
    {
        if(!map.count(s))
        {
            map.insert({s, nodeNum++});
            graph.emplace_back();
        }
    }
    void addEdge(string& s)
    {
        addWord(s);
        int id1 = map[s];
        for(auto& ch : s)
        {
            auto tmp = ch;
            ch = '*';
            addWord(s);
            int id2 = map[s];
            graph[id1].push_back(id2);
            graph[id2].push_back(id1);
            ch = tmp;
        }
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.3k Reading time ≈ 1 mins.

29. 两数相除

1
2
3
4
5
6
7
8
9
越界问题只要对除数是1和-1单独讨论就完事了啊
关于如何提高效率快速逼近结果
举个例子：11 除以 3 。
首先11比3大，结果至少是1， 然后我让3翻倍，就是6，发现11比3翻倍后还要大，那么结果就至少是2了，那我让这个6再翻倍，得12，11不比12大，吓死我了，差点让就让刚才的最小解2也翻倍得到4了。但是我知道最终结果肯定在2和4之间。也就是说2再加上某个数，这个数是多少呢？我让11减去刚才最后一次的结果6，剩下5，我们计算5是3的几倍，也就是除法，看，递归出现了。说得很乱，不严谨，大家看个大概，然后自己在纸上画一画，或者直接看我代码就好啦！

作者：liujin-4
链接：https://leetcode-cn.com/problems/divide-two-integers/solution/po-su-de-xiang-fa-mei-you-wei-yun-suan-mei-you-yi-/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
1
2
3
整理了一下思路，可以简单概括为： 60/8 = (60-32)/8 + 4 = (60-32-16)/8 + 2 + 4 = 1 + 2 + 4 = 7
    
leetcode@byMax(https://leetcode-cn.com/u/shellbye/)

溢出的情况只有负数最大除以-1会溢出，因为INT_MAX比INT_MIN绝对值小1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int divide(int dividend, int divisor) {
        if(dividend == 0)
            return 0;
        if(divisor == 1)
            return dividend;
        if(divisor == -1)
            return dividend == INT_MIN ? INT_MAX : -dividend;
        int sign = 1;
        if((dividend > 0 && divisor < 0) || (dividend < 0 && divisor > 0))
            sign = -1;
        long a = abs(dividend); // 转成long，防止溢出
        long b = abs(divisor);
        return sign * div(a, b);
    }
private:
    int div(long dividend, long divisor)
    {
        if(dividend < divisor)
            return 0;
        int c = 1;
        long oriDivisor = divisor;
        while(divisor + divisor < dividend)
        {
            c += c;
            divisor += divisor;
        }
        return c + div(dividend - divisor, oriDivisor);
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.3k Reading time ≈ 1 mins.

165. 比较版本号

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class Solution {
public:
    int compareVersion(string version1, string version2) {
        vector<int> v1;
        vector<int> v2;
        int vt = 0;
        for(auto& ch : version1)
        {
            if(ch == '.')
            {
                v1.push_back(vt);
                vt = 0;
            }
            else
            {
                vt = vt * 10 + ch - '0';
            }
        }
        v1.push_back(vt);
        while(!v1.empty() && v1.back() == 0)
            v1.pop_back();
        vt = 0;
        for(auto& ch : version2)
        {
            if(ch == '.')
            {
                v2.push_back(vt);
                vt = 0;
            }
            else
            {
                vt = vt * 10 + ch - '0';
            }
        }
        v2.push_back(vt);
        while(!v2.empty() && v2.back() == 0)
            v2.pop_back();
        int m = v1.size(), n = v2.size();
        for(int i = 0; i < min(m, n); ++i)
        {
            if(v1[i] > v2[i])
                return 1;
            else if(v1[i] < v2[i])
                return -1;
        }
        if(m > n)
            return 1;
        else if(m < n)
            return -1;
        return 0;
    }
};
优化空间，分割过程中比较
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int compareVersion(string version1, string version2) {
        int i = 0, j = 0;
        int m = version1.size(), n = version2.size();
        while(i < m || j < n)
        {
            int x = 0;
            while(i < m && version1[i] != '.')
                x = x * 10 + version1[i++] - '0';
            int y = 0;
            while(j < n && version2[j] != '.')
                y = y * 10 + version2[j++] - '0';
            if(x != y)
                return x > y ? 1 : -1;
            ++i;
            ++j;
        }
        return 0;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 2.6k Reading time ≈ 2 mins.

25. K 个一组翻转链表

递归

递归栈需要O(n / k)的空间复杂度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        if(!head)
            return nullptr;
        auto tail = head;
        ListNode* pre = nullptr;
        ListNode* pt = head;
        for(int i = 0; i < k; ++i)
            if(!pt)
                return head;
            else
                pt = pt->next;
        for(int i = 0; i < k; ++i)
        {
            if(!head)
                break;
            auto next = head->next;
            head->next = pre;
            pre = head;
            head = next;
        }
        tail->next = reverseKGroup(head, k);
        return pre;
    }
};

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        ListNode* pseudoHead = new ListNode();
        pseudoHead->next = head;
        ListNode* tail;
        auto pre = pseudoHead;
        while(pre)
        {
            ListNode* hair = pre;
            for(int i = 0; i < k; ++i)
            {
                pre = pre->next;
                if(!pre)
                    return pseudoHead->next;
            }
            auto next = pre->next;
            tie(head, tail) = reverse(hair->next, next);
            hair->next = head;
            tail->next = next;
            pre = tail;
        }
        return pseudoHead->next;
    }
private:
    pair<ListNode*, ListNode*> reverse(ListNode* head, ListNode* tail)
    {
        ListNode* pre = nullptr;
        ListNode* pt = head;
        while(pt != tail)
        {
            auto next = pt->next;
            pt->next = pre;
            pre = pt;
            pt = next;
        }
        return {pre, head};
    }
};

穿针引线

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        if(k == 1)
            return head;
        ListNode ret;
        ListNode *dummyHead{&ret};
        ret.next = head;
        auto pre = dummyHead;
        int count{k};
        while(head)
        {
            auto tmp = head;
            int c = k;
            while(c--)
            {
                if(!tmp)
                    return ret.next;
                tmp = tmp->next;
            }
            while(--count)
            {
                auto next = head->next;
                if(next)
                {
                    head->next = next->next;
                    next->next = pre->next;
                }
                else
                    head->next = nullptr;
                pre->next = next;
            }
            pre = head;
            head = head->next;
            count = k;
        }
        return ret.next;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 224 Reading time ≈ 1 mins.

58. 最后一个单词的长度

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int lengthOfLastWord(string s) {
        int end = s.size() - 1;
        int ret = 0;
        while(s[end] == ' ')
            --end;
        while(end >= 0 && s[end--] != ' ')
            ++ret;
        return ret;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 458 Reading time ≈ 1 mins.

面试题 10.01. 合并排序的数组

slot往前跑不可能跑的比ptA快，如果slot跑进A的原始领地，如果侵占了n个，那表示也用了n个A，所以A的指针永远在slot前

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    void merge(vector<int>& A, int m, vector<int>& B, int n) {
        int slot = m + n - 1;
        int ptA = m - 1;
        int ptB = n - 1;
        while(ptA >= 0 && ptB >= 0)
        {
            if(A[ptA] > B[ptB])
                A[slot--] = A[ptA--];
            else
                A[slot--] = B[ptB--];
        }
        while(slot >= 0)
        {
            if(ptA >= 0)
                A[slot--] = A[ptA--];
            else
                A[slot--] = B[ptB--];
        }
    }
};