Cinte's Leetcode Record
0%

Posted on Edited on In Disqus:
Symbols count in article: 3.8k Reading time ≈ 3 mins.

面试题 08.12. 八皇后

BackTrack
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<string>> ret;
        vector<int> pos(n);
        vector<string> tmp;
        // 从最后一行往前走
        backTrack(ret, pos, n - 1, n, tmp);
        return ret;
    }
private:
    void backTrack(vector<vector<string>>& ret, vector<int>& pos, int curLine, int n, vector<string>& tmp)
    {
        // 如果所有行都走完了，就push入结果
        if(curLine < 0)
        {
            ret.push_back(tmp); 
            return;
        }
        vector<int> avl(n, 0); // 记录已经被占用的位置
        // 遍历之前行，获取到不能放置的位置
        for(int i = n - 1; i > curLine; --i)
        {
            avl[pos[i]] = 1;
            int diff = i - curLine;
            if(pos[i] - diff >= 0)
                avl[pos[i] - diff] = 1;
            if(pos[i] + diff < n)
                avl[pos[i] + diff] = 1;
        }
        for(int i = 0; i < n; ++i)
        {
            if(avl[i]) // 如果位置被占用了，就跳过
                continue;
            pos[curLine] = i;
            tmp.push_back(getLine(i, n));
            backTrack(ret, pos, curLine - 1, n, tmp); // 进入下一行
            tmp.pop_back();
        }
        return;
    }
    string getLine(int pos, int n)
    {
        string line;
        int j = 0;
        for(j; j < pos; ++j)
            line += ".";
        line += "Q";
        while(++j < n)
            line += ".";
        return line;
    }
};
Solution

以上对于已经占用的位置需要消耗掉O(n)的时间复杂度，但是可以观察到

同一条斜线上的行和列之差或之和相等且独一无二，因此只需要记录之差和之和即可判断是否在同一斜线，时间复杂度降为O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<string>> ret;
        vector<int> pos(n);
        col = vector<int>(n, 0);
        backTrack(ret, pos, n - 1, n);
        return ret;
    }
private:
    vector<int> col;
    unordered_set<int> lx;
    unordered_set<int> rx;
    void backTrack(vector<vector<string>>& ret, vector<int>& pos, int curLine, int n)
    {
        if(curLine < 0)
        {
            ret.push_back(getBoard(pos, n));
            return;
        }
        for(int i = 0; i < n; ++i)
        {
            if(col[i] || lx.find(i - curLine) != lx.end() || rx.find(i + curLine) != rx.end())
                continue;
            pos[curLine] = i;
            col[i] = 1;
            lx.insert(i - curLine); // 记录向左上方的斜线，斜线上行列之差相等
            rx.insert(i + curLine); // 记录向右上方的斜线，斜线上行列之和相等
            backTrack(ret, pos, curLine - 1, n);
            col[i] = 0;
            lx.erase(i - curLine);
            rx.erase(i + curLine);
        }
        return;
    }
    vector<string> getBoard(vector<int> pos, int n)
    {
        vector<string> ret;
        for(auto& p : pos)
            ret.push_back(getLine(p, n));
        return ret;
    }
    string getLine(int pos, int n)
    {
        string line;
        int j = 0;
        for(j; j < pos; ++j)
            line += ".";
        line += "Q";
        while(++j < n)
            line += ".";
        return line;
    }
};

T(n) : O(n!)

S(n) : O(n)

使用位运算优化S(n)为O(1)

左边斜线就是上几行皇后位置左移行之差次，右边斜线就是上几行皇后位置右移行之差次。

对于每行，获得左斜线就是左边值左移，右斜线就是右边值右移。即可

具体看解析

x & (x - 1)将最低位1置0

x & -x就是最低位1的位置

二进制中相反数就是按位取反再加一，也就是说 x & -x = x & (~x + 1)，显然可以运算后只有最低位1可以保持1，其他都是0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<string>> ret;
        vector<int> pos(n);
        backTrack(ret, pos, n - 1, n, 0, 0, 0);
        return ret;
    }
private:
    void backTrack(vector<vector<string>>& ret, vector<int>& pos, int curLine, int n, int col, int lx, int rx)
    {
        if(curLine < 0)
        {
            ret.push_back(getBoard(pos, n));
            return;
        }
        auto alP = ((1 << n) - 1) & (~(col | lx | rx)); // 1表示有空位，为了下面的循环方便
        while(alP)
        {
            int lastZero = alP & (~alP + 1);
            int po = __builtin_ctz(lastZero); // gcc __buildin__函数，获取末尾0的数量，这里不能获取前导0，因为前导0会根据int为32位计算
            alP &= alP - 1; // 去除最后一个1，继续
            pos[curLine] = n - po - 1;
            backTrack(ret, pos, curLine - 1, n, col | lastZero, (lx | lastZero) << 1, (rx | lastZero) >> 1);
        }
        return;
    }
    vector<string> getBoard(vector<int> pos, int n)
    {
        vector<string> ret;
        for(auto& p : pos)
            ret.push_back(getLine(p, n));
        return ret;
    }
    string getLine(int pos, int n)
    {
        string line;
        int j = 0;
        for(j; j < pos; ++j)
            line += ".";
        line += "Q";
        while(++j < n)
            line += ".";
        return line;
    }
};

T(n) : O(n!)

S(n) : O(1)

Posted on Edited on In Disqus:
Symbols count in article: 993 Reading time ≈ 1 mins.

面试题 08.07. 无重复字符串的排列组合

BackTrack
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<string> permutation(string S) {
        vector<string> ret;
        string tmp;
        vector<int> visited(S.size());
        backTrack(ret, S, tmp, visited);
        return ret;
    }
private:
    void backTrack(vector<string>& ret, string& S, string& tmp, vector<int>& visited)
    {
        if(tmp.size() == S.size())
        {
            ret.push_back(tmp);
            return;
        }
        for(int i = 0; i < S.size(); ++i)
        {
            if(visited[i])
                continue;
            tmp += S[i];
            visited[i] = 1;
            backTrack(ret, S, tmp, visited);
            tmp.pop_back();
            visited[i] = 0;
        }
    }
};

一种基于交换的思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<string> permutation(string S) {
        helper(S, 0, S.size());
        return vector<string>(ret.begin(), ret.end());
    }
private:
    unordered_set<string> ret;
    void helper(string& S, int start, int n)
    {
        for(int i = start; i < n; ++i)
        {
            swap(S[start], S[i]);
            ret.insert(S);
            helper(S, start + 1, n);
            swap(S[start], S[i]);
        }
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 797 Reading time ≈ 1 mins.

面试题 08.03. 魔术索引

easy的我都做不出了

稍加优化的遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int findMagicIndex(vector<int>& nums) {
        for(int i = 0; i < nums.size(); ++i)
        {
            if(nums[i] == i)
                return i;
            if(nums[i] > i) // 重要，利用了递增序列的性质
                i = nums[i] - 1; // 如果nums[i] > i，最好的情况是i后面直到正确答案都等于nums[i],这时候跳转过去就是正确答案，但是如果后面存在严格递增的子串，则正确答案一定再nums[i]位置后面
        }
        return -1;
    }
};
伪二分的DQ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int findMagicIndex(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }
private:
    int helper(vector<int>& nums, int lo, int hi)
    {
        if(lo > hi)
            return -1;
        int mid = lo + (hi - lo) / 2;
        int left = helper(nums, lo, mid - 1);
        int right;
        if(nums[mid] == mid) // 如果中间的为mid，由于需要求最左，所以右边区间可以直接不算了
            right = mid;
        else
            right = helper(nums, mid + 1, hi);
        if(left == -1)
            return right;
        else
            return left;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 494 Reading time ≈ 1 mins.

面试题 10.05. 稀疏数组搜索

本质在于碰到""后缩减搜索区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int findString(vector<string>& words, string s) {
        int lo = 0, hi = words.size();
        while(lo <= hi)
        {
            int mid = lo + (hi - lo) / 2;
            if(words[lo] == "")
            {
                ++lo;
                continue;
            }
            if(words[hi] == "")
            {
                --hi;
                continue;
            }
            while(mid < hi && words[mid] == "")
                ++mid;
            if(words[mid] > s)
                hi = mid - 1;
            else if(words[mid] < s)
                lo = mid + 1;
            else
                return mid;
        }
        return -1;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.9k Reading time ≈ 2 mins.

面试题 10.03. 搜索旋转数组

边界条件真复杂。结合剑指 Offer 11. 旋转数组的最小数字 | Cinte's Leetcode Record思考

继续结合套路【旋转数组】从易到难，各个击破！ - 搜索旋转数组 - 力扣（LeetCode） (leetcode-cn.com)

对于一个旋转数组，分为2种，一种是出于旋转节点右边，一种是处于旋转节点左边。

当arr[lo] == arr[target]时，直接返回

当arr[mid] < arr.back()时，处于旋转节点右边

  1. arr[mid] > target : 此时target必定处于旋转节点右边一部分，那么hi = mid - 1
  2. arr[mid] < target : 此时target有两种情况
    1. target >= arr[0] : 表示了target处于0 ~ mid，则hi = mid - 1
    2. target < arr[0] : 表示了target处于mid ~，则lo = mid + 1

当arr[mid] > arr.back()时，处于旋转节点左边

  1. arr[mid] < target : 此时target必定位于旋转节点左边，是lo = mid + 1
  2. arr[mid] > target : 此时target有两种情况
    1. target >= arr[0] : 表示了target处于0 ~ mid，则hi = mid - 1
    2. target < arr[0] : 表示了target处于mid ~，则lo = mid + 1

重点

arr[mid] == target时，hi = mid，使其向左缩

重点2

当arr[mid] == arr.back()时，存在2种不确定的可能，对于这种情况需要单独处理，做法就是收缩区间。

那收缩区间是收缩lo还是hi呢，这里选择移动lo，因为所求的是最左的边界值，如果在前面没有返回的话，说明arr[lo]必定小于target，所以++lo后是安全的。

由此便可以进行二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    int search(vector<int>& arr, int target) {
        int lo = 0, hi = arr.size() - 1;
        while(lo <= hi)
        {
            if(arr[lo] == target)
                return lo;
            int mid = lo + (hi - lo) / 2;
            if(arr[mid] == target)
                hi = mid;
            else if(arr[mid] < arr.back())
            {
                if(arr[mid] > target)
                    hi = mid - 1;
                else
                {
                    if (target >= arr[0])
                        hi = mid - 1;
                    else
                        lo = mid + 1;
                }
            }else if(arr[mid] > arr.back())
            {
                if(arr[mid] < target)
                    lo = mid + 1;
                else
                {
                    if(target >= arr[0])
                        hi = mid - 1;
                    else
                        lo = mid + 1;
                }
            }else
                ++lo;
        }
        return -1;
    }
};

review

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    int search(vector<int>& arr, int target) {
        size_t lo{0}, hi{arr.size()};
        while(lo < hi) {
            auto mid{lo + (hi - lo) / 2};
            if(arr[lo] == target)
                return lo;
            if(arr[mid] > arr.back()) {
                if(arr[mid] < target)
                    lo = mid + 1;
                else {
                    if(target > arr.back())
                        hi = mid;
                    else
                        lo = mid + 1;
                }
            }else if(arr[mid] < arr.back()){
                if(arr[mid] >= target)
                    hi = mid;
                else {
                    if(target > arr.back())
                        hi = mid;
                    else
                        lo = mid + 1;
                }
            }else
                ++lo;
        }
        return (hi == arr.size() || arr[hi] != target) ? -1 : hi;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 344 Reading time ≈ 1 mins.

面试题 08.11. 硬币

设F(i, v)为前i种面值硬币构成面额为v的方案数。

(题中i为4，且面额为[1, 5, 10, 25])

将第i个面额记为c_i

则转移方程 \[ F(i, v) = F(i - 1, v - 0 * c_i) + F(i - 1, v - 1 * c_i) + F(i - 1, v - 2 * c_i) + ... + F(i - 1, v - v/c_i * c_i) \]

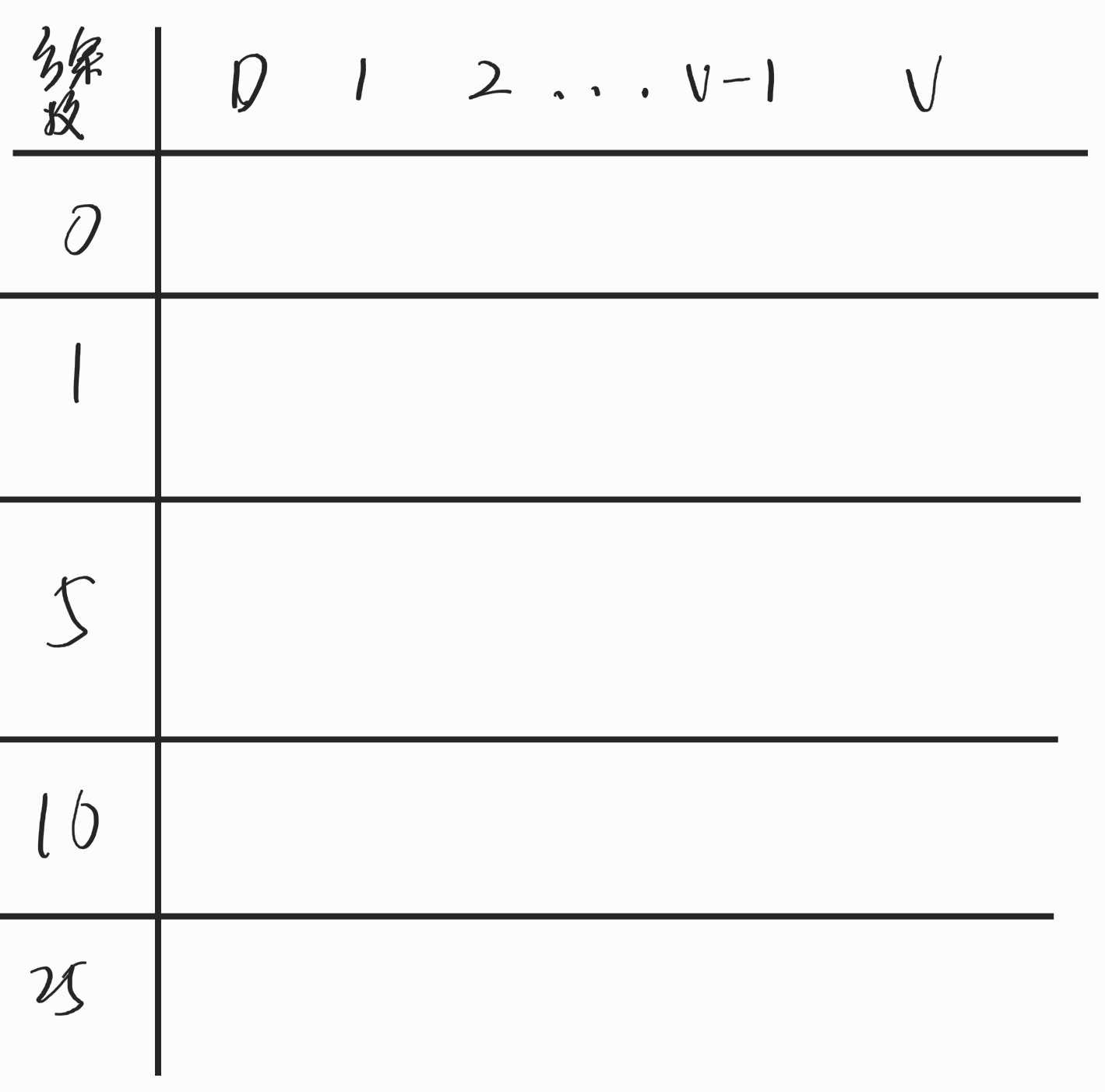
这是一个纵轴为采用的硬币种类，横轴为面额，内部值为方案数的表格

以上的原始版本的代码实现

以上的原始版本的代码实现 

class Solution {
public:
    int waysToChange(int n) {
        int coins[4]{1, 5, 10, 25};
        vector> dp(5, vector(n + 1, 0));
        dp[0][0] = 1;
        for(int i = 1; i <= 4; ++i)
        {
            dp[i][0] = 1;
            auto coin = coins[i - 1];
            for(int j = 1; j <= n; ++j)
            {
                dp[i][j] = dp[i - 1][j];
                for(int k = 1; k <= j / coin; ++k)
                {
                    dp[i][j] += dp[i - 1][j - k * coin];
                    dp[i][j] %= 1000000007;
                }
            }
        }
        return dp.back().back();
    }
};

但是超时了

进行对时间的优化 \[ F(i, v) = F(i - 1, v - 0 * c_i) + F(i - 1, v - 1 * c_i) + F(i - 1, v - 2 * c_i) + ... + F(i - 1, v - v/c_i * c_i) \] 图中标红的公式与 \[ F(i, v - c_i) = F(i - 1, v - 1 * c_i) + F(i - 1, v - 2 * c_i) + ... + F(i - 1, v - v/c_i * c_i) \] 进行比较，发现相同，所以 \[ F(i, v) = F(i - 1, v - 0 * c_i) + F(i, v - c_i) \] 于是就可以减少一层循环
以上的优化时间版本的代码实现 

class Solution {
public:
    int waysToChange(int n) {
        int coins[4]{1, 5, 10, 25};
        vector> dp(5, vector(n + 1, 0));
        dp[0][0] = 1;
        for(int i = 1; i <= 4; ++i)
        {
            dp[i][0] = 1;
            auto coin = coins[i - 1];
            for(int j = 1; j <= n; ++j)
            {
                dp[i][j] = dp[i - 1][j];
                if(j >= coin)
                    dp[i][j] += dp[i][j - coin];
                dp[i][j] %= 1000000007;
            }
        }
        return dp.back().back();
    }
};

对空间优化

发现每次循环仅仅使用到了上一层的数据，因此可以将空间使用从二维减少到一维，就用常规的方式即可

最终版本的代码

T(n) : O(n)

S(n) : O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int waysToChange(int n) {
        int coins[4]{1, 5, 10, 25};
        vector<int> dp(n + 1, 0);
        dp[0] = 1;
        for(int i = 1; i <= 4; ++i)
        {
            auto coin = coins[i - 1];
            for(int j = coin; j <= n; ++j)
            {
                dp[j] = dp[j] + dp[j - coin];
                dp[j] %= 1000000007;
            }
        }
        return dp.back();
    }
};

还有数学方法，抄累了

Posted on Edited on In Disqus:
Symbols count in article: 542 Reading time ≈ 1 mins.

面试题 05.03. 翻转数位

一个dp问题(我又菜起来了)

curSum记录当前遇到的连续的1。 curSumF记录翻转过后最长的连续1。

遇到0

​ curSum置0。

​ curSumF置为curSum+1，表示连接了前面一段。

遇到1

​ curSum和curSumF都加1。

因为curSum始终记录这前面一段连续1，所以设置为curSum+1后，如果后面还连续，就会自动更新连接这两段，如果后面为1，那就会清空为仅翻转当前位。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int reverseBits(int num) {
        int curSum = 0;
        int curSumF = 0;
        int ret = 0;
        int i = 0;
        while(i++ < 32)
        {
            if(num & 1)
            {
                ++curSum;
                ++curSumF;
            }else
            {
                curSumF = curSum + 1;
                curSum = 0;
            }
            num >>= 1; // 这里用右移，例如2147483647左移不让移
            ret = max(ret, curSumF);
        }
        return ret;
    }
};

类似滑动窗口

Posted on Edited on In Disqus:
Symbols count in article: 1.3k Reading time ≈ 1 mins.

面试题 04.10. 检查子树

递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool checkSubTree(TreeNode* t1, TreeNode* t2) {
        queue<TreeNode*> q;
        q.push(t1);
        while(!q.empty())
        {
            auto p = q.front();
            q.pop();
            if(check(p, t2))
                return true;
            if(p->left)
                q.push(p->left);
            if(p->right)
                q.push(p->right);
        }
        return false;
    }
private:
    bool check(TreeNode* t1, TreeNode* t2)
    {
        if(!t1)
            return !t2;
        if(!t2)
            return !t1;
        if(t1->val != t2->val)
            return false;
        return check(t1->left, t2->left) && check(t1->right, t2->right);
    }
};

递归改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool checkSubTree(TreeNode* t1, TreeNode* t2) {
        if(!t1)
            return !t2;
        return check(t1, t2) || checkSubTree(t1->left, t2) || checkSubTree(t1->right, t2);
    }
private:
    bool check(TreeNode* t1, TreeNode* t2)
    {
        if(!t1)
            return !t2;
        if(!t2)
            return !t1;
        if(t1->val != t2->val)
            return false;
        return check(t1->left, t2->left) && check(t1->right, t2->right);
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 3.1k Reading time ≈ 3 mins.

面试题 03.06. 动物收容所

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
class AnimalShelf {
public:
    AnimalShelf() : head(new Node()), tail(new Node()) {
        head->next = tail;
        tail->prev = head;
    }
    
    void enqueue(vector<int> animal) {
        push(animal[0], animal[1]);
    }
    
    vector<int> dequeueAny() {
        if(tail->prev == head)
            return {-1, -1};
        vector<int> ret{tail->prev->num, tail->prev->type};
        deleteNode(tail->prev);
        return ret;
    }
    
    vector<int> dequeueDog() {
        auto ret = pop(1);
        if(ret == -1)
            return {-1, -1};
        return {ret, 1};
    }
    
    vector<int> dequeueCat() {
        auto ret = pop(0);
        if(ret == -1)
            return {-1, -1};
        return {ret, 0};
    }
private:
    struct Node
    {
        Node* next;
        Node* prev;
        int num = 0;
        int type;
        Node() = default;
        Node(Node* next, Node* prev, int num, int type) : next(next), prev(prev), num(num), type(type) {};
    };
    Node *head, *tail;
    void push(int num, int type)
    {
        auto next = head->next;
        head->next = new Node(head->next, head, num, type);
        next->prev = head->next;
    }
    int pop(int type)
    {
        auto point = tail->prev;
        while(point != head)
        {
            if(point->type == type)
            {
                auto ret = point->num;
                deleteNode(point);
                return ret;
            }
            point = point->prev;
        }
        return -1;
    }
    void deleteNode(Node* node)
    {
        auto tmp = node;
        node->prev->next = node->next;
        node->next->prev = node->prev;
        delete tmp;
    }
};

/**
 * Your AnimalShelf object will be instantiated and called as such:
 * AnimalShelf* obj = new AnimalShelf();
 * obj->enqueue(animal);
 * vector<int> param_2 = obj->dequeueAny();
 * vector<int> param_3 = obj->dequeueDog();
 * vector<int> param_4 = obj->dequeueCat();
 */

题目没写出来，编号是有先后的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class AnimalShelf {
public:
    AnimalShelf() {

    }
    
    void enqueue(vector<int> animal) {
        if(animal[1] == 0)
            cat.push_back(animal[0]);
        else
            dog.push_back(animal[0]);
    }
    
    vector<int> dequeueAny() {
        if(dog.empty() && cat.empty())
            return {-1, -1};
        if(dog.empty())
        {
            auto ret = cat.front();
            cat.pop_front();
            return {ret, 0};
        }else if(cat.empty())
        {
            auto ret = dog.front();
            dog.pop_front();
            return {ret, 1};
        }else if(dog.front() < cat.front())
        {
            auto ret = dog.front();
            dog.pop_front();
            return {ret, 1};
        }else
        {
            auto ret = cat.front();
            cat.pop_front();
            return {ret, 0};
        }
    }
    
    vector<int> dequeueDog() {
        if(dog.empty())
            return {-1, -1};
        auto ret = dog.front();
        dog.pop_front();
        return {ret, 1};
    }
    
    vector<int> dequeueCat() {
        if(cat.empty())
            return {-1, -1};
        auto ret = cat.front();
        cat.pop_front();
        return {ret, 0};
    }
private:
    deque<int> cat;
    deque<int> dog;
};

/**
 * Your AnimalShelf object will be instantiated and called as such:
 * AnimalShelf* obj = new AnimalShelf();
 * obj->enqueue(animal);
 * vector<int> param_2 = obj->dequeueAny();
 * vector<int> param_3 = obj->dequeueDog();
 * vector<int> param_4 = obj->dequeueCat();
 */

Posted on Edited on In Disqus:
Symbols count in article: 336 Reading time ≈ 1 mins.

面试题 05.02. 二进制数转字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    string printBin(double num) {
        int i = 0;
        string ret = "0.";
        while(num && i++ < 30)
        {
            num *= 2;
            if(num >= 1)
            {
                ret.append("1");
                num -= 1;
            }else
                ret.append("0");
        }
        if(num != 0)
            return "ERROR";
        else
            return ret;
    }
};