Cinte's Leetcode Record
0%

Posted on Edited on In Disqus:
Symbols count in article: 798 Reading time ≈ 1 mins.

108. Convert Sorted Array to Binary Search Tree

直接递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }
private:
    TreeNode* helper(vector<int>& nums, int start, int end)
    {
        if(start > end)
            return nullptr;
        int mid = (start + end) >> 1;
        TreeNode* node = new TreeNode(nums[mid]);
        node->left = helper(nums, start, mid - 1);
        node->right = helper(nums, mid + 1, end);
        return node;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 2.6k Reading time ≈ 2 mins.

103. Binary Tree Zigzag Level Order Traversal

使用双向队列，每次都变向
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        if(!root)
            return {};
        vector<vector<int>> ret;
        deque<TreeNode*> s;
        s.push_back(root);
        bool left = false;
        int l = 1;
        while(!s.empty())
        {
            int t = s.size();
            vector<int> tmp;
            while(t-- > 0)
            {
                TreeNode* p;
                if(left)
                {
                    p = s.front();
                    s.pop_front();
                    if(p->right)
                        s.push_back(p->right);
                    if(p->left)
                       s.push_back(p->left);
                }else
                {
                    p = s.back();
                    s.pop_back();
                    if(p->left)
                        s.push_front(p->left);
                    if(p->right)
                       s.push_front(p->right);
                }
                tmp.push_back(p->val);
            }
            ret.push_back(tmp);
            left = !left;
        }
        return ret;
    }
};

review

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        if(!root)
            return {};
        deque<TreeNode*> dq;
        dq.push_back(root);
        vector<vector<int>> ret;
        while(!dq.empty())
        {
            ret.emplace_back();
            for(int i = 0, sz = dq.size(); i < sz; ++i)
            {
                auto node = dq.front();
                dq.pop_front();
                if(node->left)
                    dq.push_back(node->left);
                if(node->right)
                    dq.push_back(node->right);
                ret.back().push_back(node->val);
            }
            if(dq.empty())
                break;
            ret.emplace_back();
            for(int i = 0, sz = dq.size(); i < sz; ++i)
            {
                auto node = dq.back();
                dq.pop_back();
                if(node->right)
                    dq.push_front(node->right);
                if(node->left)
                    dq.push_front(node->left);
                ret.back().push_back(node->val);
            }
        }
        return ret;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 694 Reading time ≈ 1 mins.

88. Merge Sorted Array

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int i = m - 1, j = n - 1, k = m + n - 1;
        while(i >= 0 && j >= 0)
        {
            if(nums1[i] > nums2[j])
                nums1[k--] = nums1[i--];
            else
                nums1[k--] = nums2[j--];
        }
        while(j >= 0)
            nums1[k--] = nums2[j--];
    }
};

大的全放后面，小的就留在前面

review

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int i = m - 1, j = n - 1, k = m + n - 1;
        while(k >= 0)
        {
            if(i < 0)
                nums1[k--] = nums2[j--];
            else if(j < 0)
                nums1[k--] = nums1[i--];
            else if(nums1[i] > nums2[j])
                nums1[k--] = nums1[i--];
            else
                nums1[k--] = nums2[j--];
        }
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.8k Reading time ≈ 2 mins.

91. Decode Ways

dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    int numDecodings(string s) {
        if(s.empty())
            return 0;
        vector<int> memo(s.size() + 1, 0);
        memo[0] = 1;
        memo[1] = s[0] != '0';
        for(int i = 1; i < s.size(); ++i)
        {
            if(memo[i] && s[i] != '0')
                memo[i + 1] += memo[i];
            if(memo[i - 1] && map.find(s.substr(i - 1, 2)) != map.end())
                memo[i + 1] += memo[i - 1];
        }
        return memo.back();
    }
private:
    unordered_set<string> map
    {
        "1",
        "2", 
        "3", 
        "4", 
        "5", 
        "6", 
        "7", 
        "8", 
        "9", 
        "10", 
        "11", 
        "12", 
        "13", 
        "14", 
        "15", 
        "16", 
        "17", 
        "18", 
        "19",
        "20", 
        "21", 
        "22", 
        "23",
        "24", 
        "25", 
        "26",
    };
};

每步检查当前的是否符合，如果符合，继承前一个的路数。

当前和前一个叠加的是否符合，如果符合，继承前前的路数

路数是相加的，因为这里分叉了

不用set
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int numDecodings(string s) {
        if(s.empty())
            return 0;
        vector<int> memo(s.size() + 1, 0);
        memo[0] = 1;
        memo[1] = s[0] != '0';
        for(int i = 1; i < s.size(); ++i)
        {
            if(memo[i] && s[i] != '0')
                memo[i + 1] += memo[i];
            if(memo[i - 1] && stoi(s.substr(i - 1, 2)) <= 26 && stoi(s.substr(i - 1, 2)) >= 10)
                memo[i + 1] += memo[i - 1];
        }
        return memo.back();
    }    
};

review 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int numDecodings(string s) {
        if(s.empty())
            return 0;
        int n = s.size();
        vector<int> dp(n + 1);
        dp[0] = 1;
        dp[1] = s[0] != '0';
        for(int i = 1; i < n; ++i)
        {
            if(s[i] != '0')
                dp[i + 1] += dp[i];
            int num = (s[i - 1] - '0') * 10 + (s[i] - '0');
            if(10 <= num && num <= 26)
                dp[i + 1] += dp[i - 1];
        }
        return dp.back();
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.2k Reading time ≈ 1 mins.

74. Search a 2D Matrix

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int i = m - 1, j = 0;
        while(i >= 0 && j < n)
        {
            if(matrix[i][j] < target)
                ++j;
            else if(matrix[i][j] > target)
                --i;
            else 
                return true;
        }
        return false;
    }
};

O(n)

对于这种方式，由于每行每列都是有序的，所以可以先通过二分查找第一列中最后一个不大于target的数，然后在那一行中二分搜索 

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        auto row = upper_bound(matrix.begin(), matrix.end(), target, [](int a, vector<int>& v){
            return a < v[0];
        }); // 注意comp是value和容器中的元素比
        if(row == matrix.begin())
            return false;
        --row;
        return binary_search(row->begin(), row->end(), target);
    }
};
##### 二分搜索

虽然是个二维矩阵，但是每行排开来他就是个递增数列，但是这种方法没有很好的利用他矩阵的特点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int lo = 0, hi = m * n - 1;
        while(lo < hi)
        {
            int mid = lo + (hi - lo) / 2;
            if(matrix[mid / n][mid % n] >= target)
                hi = mid;
            else
                lo = mid + 1;
        }
        return matrix[hi / n][hi % n] == target;
    }
};

O(log(m * n))

Posted on Edited on In Disqus:
Symbols count in article: 1.7k Reading time ≈ 2 mins.

343. Integer Break

dp
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1);
        dp[0] = 0;
        dp[1] = 1;
        for(int i = 2; i <= n; ++i)
            for(int j = 1; j < i; ++j)
                dp[i] = max(dp[i], max(j, dp[j]) * max(i - j, dp[i - j]));
        return dp.back();
    }
};

对于一个数，截成两段，挨个尝试，每一段由于那个数字在运算时候是不计算他本身的，所以后面用时候需要比较他自己和他break后谁打，所以要有这么多max

数学方法优化

discussion 

1
2
3
4
5
6
7
8
You're making it pretty complicated.

If an optimal product contains a factor f >= 4, then you can replace it with factors 2 and f-2 without losing optimality, as 2*(f-2) = 2f-4 >= f. So you never need a factor greater than or equal to 4, meaning you only need factors 1, 2 and 3 (and 1 is of course wasteful and you'd only use it for n=2 and n=3, where it's needed).

For the rest I agree, 3*3 is simply better than 2*2*2, so you'd never use 2 more than twice.

6 = 2 + 2 + 2 = 3 + 3. But 2 * 2 * 2 < 3 * 3.
Therefore, if there are three 2's in the decomposition, we can replace them by two 3's to gain a larger product.
存在大于4的因子时候，他永远可以被拆到小于4，因此只需要1，2，3

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1);
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 1;
        for(int i = 3; i <= n; ++i)
            dp[i] = max(3 * max(i - 3, dp[i - 3]) ,max(dp[i - 1], 2 * max(i - 2, dp[i - 2]))); // 此处dp[i - 1]而不是max(dp[i - 1], i - 1)是因为i>3时，2 * (i - 2) > 1 * (i - 1)
        return dp.back();
    }
};

空间优化 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1);
        int a = 0;
        int b = 1;
        int c = 1;
        for(int i = 3; i <= n; ++i)
        {
            a = max(max(dp[i - 1], max(i - 2, dp[i - 2]) * 2), max(a, i - 3) * 3);
            swap(a, b);
            swap(b, c);
        }
        return c;
    }
};
##### 纯数学 
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int integerBreak(int n) {
        if(n <= 3)
            return n - 1;
        int a = n / 3, b = n % 3;
        if(b == 1)
            return pow(3, a - 1) * 4;
        if(b == 2)
            return pow(3, a) * 2;
        return pow(3, a);
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 808 Reading time ≈ 1 mins.

304. Range Sum Query 2D - Immutable

dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
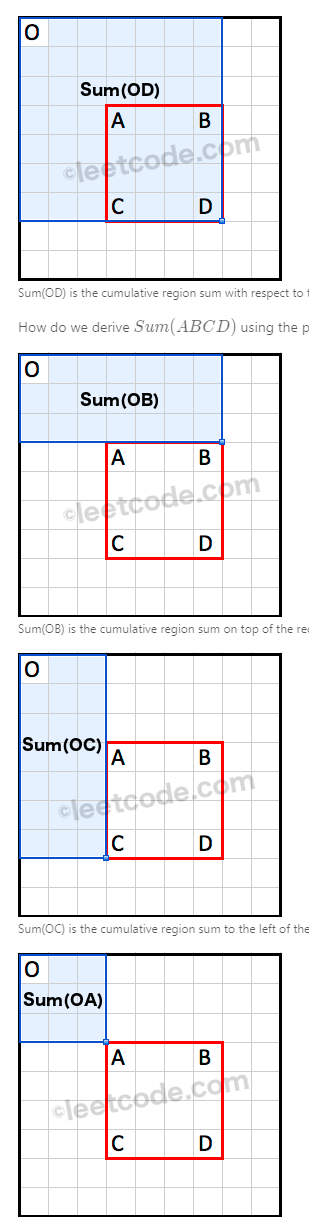
class NumMatrix {
public:
    NumMatrix(vector<vector<int>>& matrix) : dp(vector<vector<int>>(matrix.size() + 1, vector<int>(matrix[0].size() + 1, 0))), rows(matrix.size()), cols(matrix[0].size()) {
        for(int i = 1; i < rows + 1; ++i)
        {
            for(int j = 1; j < cols + 1; ++j)
            {
                dp[i][j] = matrix[i - 1][j - 1] + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return dp[row2 + 1][col2 + 1] - dp[row1][col2 + 1]- dp[row2 + 1][col1] + dp[row1][col1];
    }
private:
    vector<vector<int>> dp;
    int rows, cols;
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * int param_1 = obj->sumRegion(row1,col1,row2,col2);
 */

大小加一时为了防止下标越界

1621411468268.png

Posted on Edited on In Disqus:
Symbols count in article: 625 Reading time ≈ 1 mins.

264. Ugly Number II

dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int nthUglyNumber(int n) {
        vector<int> dp(n);
        dp[0] = 1;
        int l1 = 0, l2 = 0, l3 = 0;
        for(int i = 1; i < n; ++i)
        {
            auto t1 = dp[l1] * 2;
            auto t2 = dp[l2] * 3;
            auto t3 = dp[l3] * 5;
            dp[i] = min(min(t1, t2), t3);
            if(dp[i] == t1)
                ++l1;
            if(dp[i] == t2) // 去重，如果一个值在当前回合是最小值，那么如果存在重复，在下一回合中他也是最小值，因此需要去重。不能用else if
                ++l2;       // 不仅仅是去重，还需要指针的移动
            if(dp[i] == t3)
                ++l3;
        }
        return dp.back();
    }
};

维护三个序列，分别是x2，x3，x5的序列。其中通过l1,l2,l3表示

这三个序列通过指针的位置来表示，当这个序列的用完后，根据dp中由小到大排，那么移动到下一个作为下一个的候选

之所以可以这样是因为dp已经帮助我们实现排序，因此只需要应用之前的排序结果，取了其中一个序列的一个值后，把他移动到序列的下一个位置，也就是ugly number种刚好比他大的一个数。注意三个数的序列可能会发生重叠。因此需要去重处理。

Posted on Edited on In Disqus:
Symbols count in article: 286 Reading time ≈ 1 mins.

485. 最大连续 1 的个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int findMaxConsecutiveOnes(vector<int>& nums) {
        int maxSofar = 0;
        int maxCur = 0;
        for(auto& num : nums)
        {
            if(num == 1)
            {
                ++maxCur;
                maxSofar = max(maxCur, maxSofar);
            }
            else
                maxCur = 0;
        }
        return maxSofar;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 3.6k Reading time ≈ 3 mins.

97. Interleaving String

因为如果可以实现交替，就必然满足|n - m| <= 1这个条件，所以这个条件可以不用考虑

dp:

  1. 递归
  2. 带memory的递归top-down
  3. bottom-up
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        return helper(s1, s2, s3, 0, 0, 0);
    }
private:
    bool helper(string& s1, string& s2, string& s3, int i, int j, int k)
    {
        if(i >= s1.size())
            return isEquel(s2, s3, j, k);
        if(j >= s2.size())
            return isEquel(s1, s3, i, k);
        return (s1[i] == s3[k] && helper(s1, s2, s3, i + 1, j, k + 1)) || (s2[j] == s3[k] && helper(s1, s2, s3, i, j + 1, k + 1));
    }
    bool isEquel(string& s1, string& s2, int i, int j)
    {
        if(s1.size() - i != s2.size() - j)
            return false;
        while(i < s1.size() && j < s2.size())
        {
            if(s1[i++] != s2[j++])
                return false;
        }
        return true;
    }
};

但是在递归过程中，如果有些部分有几个重复的连续串，那么就会产生运算的交叠，所以使用memo来规避已经计算过的内容

sample: 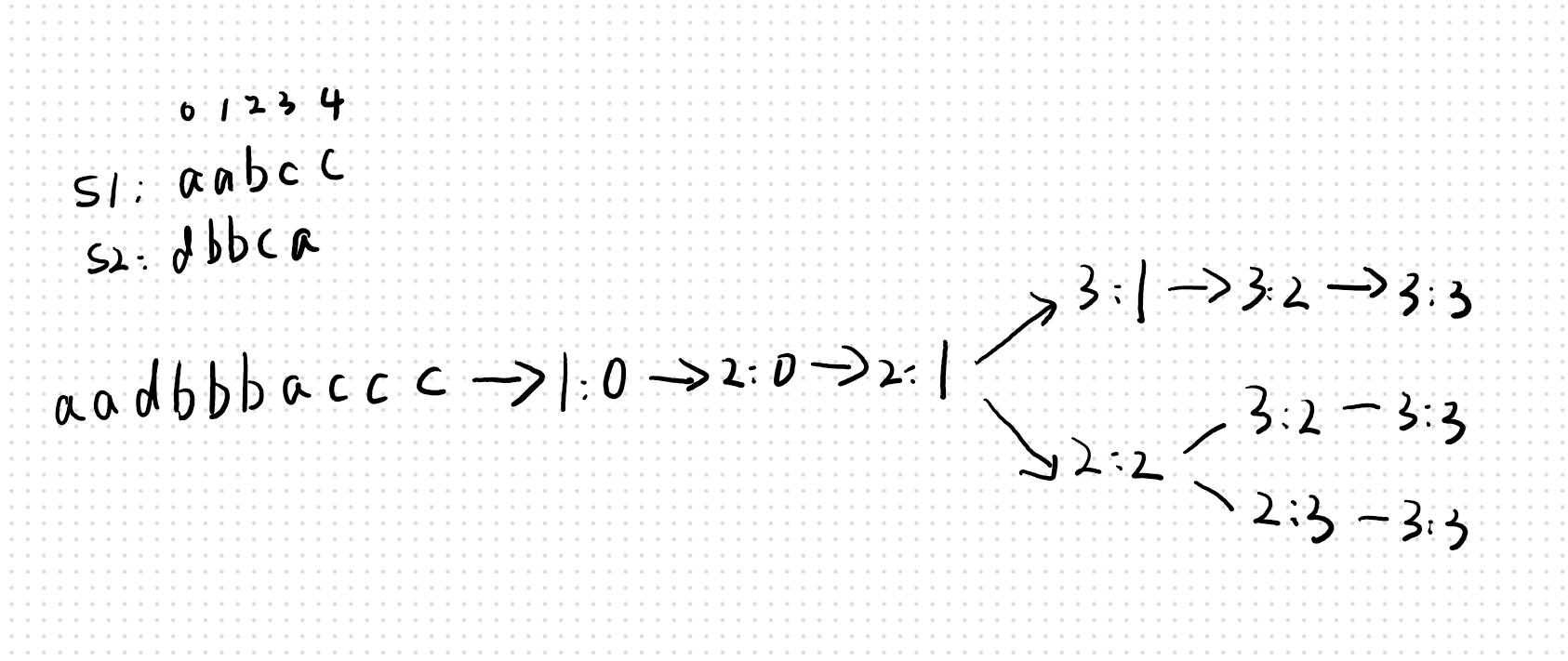1621222087208.png

top-down
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        dp = vector<vector<int>>(s1.size(), vector<int>(s2.size(), - 1));
        if(s1.size() + s2.size() != s3.size())
            return false;
        return helper(s1, s2, s3, 0, 0, 0);
    }
private:
    vector<vector<int>> dp;
    bool helper(string& s1, string& s2, string& s3, int i, int j, int k)
    {
        if(i >= s1.size())
            return isEquel(s2, s3, j, k);
        if(j >= s2.size())
            return isEquel(s1, s3, i, k);
        if(dp[i][j] >= 0)
            return dp[i][j] == 1;
        bool ans = false;
        if((s1[i] == s3[k] && helper(s1, s2, s3, i + 1, j, k + 1)) || (s2[j] == s3[k] && helper(s1, s2, s3, i, j + 1, k + 1)))
            ans = true;
        dp[i][j] = ans ? 1 : 0;
        return ans;
    }
    bool isEquel(string& s1, string& s2, int i, int j)
    {
        if(s1.size() - i != s2.size() - j)
            return false;
        while(i < s1.size())
        {
            if(s1[i++] != s2[j++])
                return false;
        }
        return true;
    }
};
bottom-up

dp[i][j]表示(0..i)的s1子串和(0..j)的s2子串，如果他们可以交错成一个(0...i+j+1)的s3子串，那么就是true

2种情况

  1. 当s1[i]!=s3[i+j+1] && s2[j]!=s3[i+j+1]，那么绝对为false，因为某尾匹配不了
  2. 当s1[i]==s3[i+j+1]时，那么结果等同于dp[i-1][j]，最后一位把s1[i]匹配走了，那么如果之前都匹配成功，就是true了，当s2[j]==s3[i+j+1]时同理

base:
当一个子串为空串时候的匹配结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        if(s1.size() + s2.size() != s3.size())
            return false;
        vector<vector<bool>> dp(s1.size() + 1, vector<bool>(s2.size() + 1, false));
        for(int i = 0; i <= s1.size(); ++i)
        {
            for(int j = 0; j <= s2.size(); ++j)
            {
                if(i == 0 && j == 0)
                    dp[i][j] = true;
                else if(i == 0)
                    dp[i][j] = dp[i][j - 1] && s2[j - 1] == s3[j - 1];
                else if(j == 0)
                    dp[i][j] = dp[i - 1][j] && s1[i - 1] == s3[i - 1];
                else
                    dp[i][j] = (s1[i - 1] == s3[i + j - 1] && dp[i - 1][j]) || (s2[j - 1] == s3[i + j - 1] && dp[i][j - 1]);

            }
        }
        return dp.back().back();
    }
};

优化空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        if(s1.size() + s2.size() != s3.size())
            return false;
        vector<bool> dp(s2.size() + 1, false);
        for(int i = 0; i <= s1.size(); ++i)
        {
            for(int j = 0; j <= s2.size(); ++j)
            {
                if(i == 0 && j == 0)
                    dp[j] = true;
                else if(i == 0)
                    dp[j] = dp[j - 1] && s2[j - 1] == s3[j - 1];
                else if(j == 0)
                    dp[j] = dp[j] && s1[i - 1] == s3[i - 1];
                else
                    dp[j] = (s1[i - 1] == s3[i + j - 1] && dp[j]) || (s2[j - 1] == s3[i + j - 1] && dp[j - 1]);

            }
        }
        return dp.back();
    }
};

review

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int m = s1.size(), n = s2.size();
        if(s3.size() != m + n)
            return false;
        if(m == 0)
            return s2 == s3;
        if(n == 0)
            return s1 == s3;
        vector<int> dp(n + 1);
        dp[0] = 1;
        for(int i = 1; i <= n; ++i)
            dp[i] = dp[i - 1] && s2[i - 1] == s3[i - 1];
        for(int i = 1; i <= m; ++i)
        {
            dp[0] = dp[0] && s1[i - 1] == s3[i - 1];
            for(int j = 1; j <= n; ++j)
                dp[j] = (s1[i - 1] == s3[i + j - 1] && dp[j]) || (s2[j - 1] == s3[i + j - 1] && dp[j - 1]);
        }
        return dp.back();
    }
};