Cinte's Leetcode Record
0%

Posted on Edited on In Disqus:
Symbols count in article: 1.8k Reading time ≈ 2 mins.

146. LRU Cache

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
class LRUCache {
public:
    LRUCache(int capacity): capacity(capacity), head(new Node()), tail(new Node()) {
        head->post = tail;
        head->prev = nullptr;
        tail->prev = head;
        tail->post = nullptr;
    }
    
    int get(int key) {
        if(cache.find(key) != cache.end())
        {
            moveNodeToHead(cache[key]);
            return cache[key]->val;
        }
        else
            return -1;
    }
    
    void put(int key, int value) {
        if(cache.find(key) == cache.end())
        {
            if(cache.size() > capacity - 1)
                cache.erase(removeTailNode());
            Node* node = new Node(key, value);
            addNodeToHead(node);
            cache[key] = node;
        }else
        {
            auto node = cache[key];
            if(node->val != value)
                node->val = value;
            moveNodeToHead(node);
        }
    }
private:
    struct Node {
        int key;
        int val;
        Node* prev;
        Node* post;
        Node() = default;
        Node(int key, int val): key(key), val(val) {}
    };
    void removeNode(Node* node)
    {
        node->prev->post = node->post;
        node->post->prev = node->prev;
    }
    void addNodeToHead(Node* node)
    {
        node->prev = head;
        node->post = head->post;
        head->post = node;
        node->post->prev = node;
    }
    void moveNodeToHead(Node* node)
    {
        removeNode(node);
        addNodeToHead(node);
    }
    int removeTailNode()
    {
        auto node = tail->prev;
        tail->prev = node->prev;
        tail->prev->post = tail;
        auto key = node->key;
        delete node;
        return key;
    }
    Node* head;
    Node* tail;
    int capacity;
    unordered_map<int, Node*> cache;
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

使用doubleLinkedList是因为在删除时候需要操作前面的元素，因此DoublelinkedList可以实现O(1)的删除操作，而SingleLinkedList就需要O(n)
总体思路是访问过的移动到第一位，而最少访问的放在最后，如果新进来的时候缓存满了，那么就释放掉最后一位。

Posted on Edited on In Disqus:
Symbols count in article: 432 Reading time ≈ 1 mins.

69. Sqrt(x)

Newton's method
1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int mySqrt(int x) {
        long r = x;
        while(r * r > x)
        {
            r = (r + x / r) / 2;
        }
        return r;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int mySqrt(int x) {
        int lo = 0, hi = x;
        while(lo < hi)
        {
            int mid = lo + (hi - lo) / 2 + 1; // 使得中点偏向右边，防止无限循环
            if(mid <= x / mid)
                lo = mid;
            else
                hi = mid - 1;
        }
        return hi;
    }
};

Tips:usemid > x / mid instead of mid * mid > x, because of the overflow

Posted on Edited on In Disqus:
Symbols count in article: 2.4k Reading time ≈ 2 mins.

148. Sort List

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    // split O(logn)
    ListNode* sortList(ListNode* head) {
        // head->next 是为了单个节点的情况
        if(!head || !head->next)
            return head;
        auto midPoint = getMid(head);
        auto left = sortList(head);
        auto right = sortList(midPoint);
        return mergeList(left, right);
    }
private:
    // 这里的获取终点函数记得要进行部分调整，要从中间切断这个list
    // O(n)
    ListNode* getMid(ListNode* head)
    {
        ListNode* walker = nullptr;
        ListNode* runner = head;
        while(runner && runner->next)
        {
            walker = !walker ? head : walker->next;
            runner = runner->next->next;
        }
        ListNode* mid = walker->next;
        walker->next = nullptr;
        return mid;
    }
    // O(n)
    ListNode* mergeList(ListNode* l1, ListNode* l2)
    {
        if(!l1)
            return l2;
        if(!l2)
            return l1;
        if(l1->val > l2->val)
        {
            l2->next = mergeList(l2->next, l1);
            return l2;
        }else
        {
            l1->next = mergeList(l1->next, l2);
            return l1;
        }
        return nullptr;
    }
};

T(n) : O(nlogn)

总体是分成许多一半一半的，然后每一小部分merge

优化merge
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* sortList(ListNode* head) {
        if(!head || !head->next)
            return head;
        auto midPoint = getMid(head);
        auto left = sortList(head);
        auto right = sortList(midPoint);
        return mergeList(left, right);
    }
private:
    ListNode* getMid(ListNode* head)
    {
        ListNode* walker = nullptr;
        ListNode* runner = head;
        while(runner && runner->next)
        {
            walker = !walker ? head : walker->next;
            runner = runner->next->next;
        }
        ListNode* mid = walker->next;
        walker->next = nullptr;
        return mid;
    }
    ListNode* mergeList(ListNode* l1, ListNode* l2)
    {
        ListNode dummyHead(0);
        auto prev = &dummyHead;
        while(l1 && l2)
        {
            if(l1->val > l2->val)
            {
                prev->next = l2;
                l2 = l2->next;
            }else
            {
                prev->next = l1;
                l1 = l1->next;
            }
            prev = prev->next;
        }
        if(l1)
            prev->next = l1;
        else
            prev->next = l2;
        return dummyHead.next;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 541 Reading time ≈ 1 mins.

876. Middle of the Linked List

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode* walker = head;
        ListNode* runner = head;
        while(runner && runner->next)
        {
            walker = walker->next;
            runner = runner->next->next;
        }
        return walker;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.4k Reading time ≈ 1 mins.

45. Jump Game II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int jump(vector<int>& nums) {
        int level = 0;
        int maxReach = 0;
        int i = 0;
        while(maxReach < nums.size() - 1)
        {
            ++level;
            for(int maxT = maxReach; i <= maxT; ++i)
            {
                maxReach = max(maxReach, nums[i] + i);
                if(maxReach >= nums.size() - 1)
                    return level;
            }
        }
        return level;
    }
};

视为BFS问题

每个区域里都可以走到下一层的任何一个点，实在走不到了，只能换层了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int jump(vector<int>& nums) {
        int level = 0, maxReachFurther = 0, maxReachEnd = 0; // #defind jumptime level，这样解释比较合理
        for(int i = 0; i < nums.size() - 1; ++i)  // 这里用nums.size() - 1而不是nums.size() 是因为如果走到了最后一个，但是最后一个，那么已经不用考虑换层了，例如[0]，如果到达0，再换层，那就扰乱了结果。因为假设的是一定可以到达终点，而最后一次起跳就表示了一定可以到达终点。这里面对最后一跳超越终点也无所谓，因为已经记录了这一跳了。
        {
            maxReachFurther = max(maxReachFurther, nums[i] + i); // 目前层能达到的最远
            // 首先先从0开始起跳，跳跃次数加一。然后每次碰到这次的结尾，跳跃次数加一。
            if(maxReachEnd == i)
            {
                maxReachEnd = maxReachFurther;  // 对于下一层来说  记录上一层能达到的最远，如果遇见，那么这一层就结束了
                ++level; // level代表着需要重新起跳，跳到下一层了，记录的不是层数而跳跃的次数。
            }
        }
        return level;
    }
};

review

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int jump(vector<int>& nums) {
        int level = 0;
        int this_level_border = 0; // 上一层所决定的这一层的边界
        int cur_reach = 0; // 当前最大能到的，下一层的边界
        int n = nums.size();
        for(int i = 0; i < n; ++i)
        {
            if(this_level_border >= n - 1)
                return level;
            cur_reach = max(cur_reach, nums[i] + i);
            if(this_level_border == i)
            {
                ++level;
                this_level_border = cur_reach;
            }
        }
        return level;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 3.4k Reading time ≈ 3 mins.

581. Shortest Unsorted Continuous Subarray

Brute Force(超时)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        int l = nums.size();
        int r = 0;
        for(int i = 0; i < nums.size(); ++i)
        {
            for(int j = i + 1; j < nums.size(); ++j)
            {
                if(nums[j] < nums[i])
                {
                    r = max(r, j);
                    l = min(l, i);
                }
            }
        }
        return l == nums.size() ? 0 : r - l + 1;
    }
};

o(n^2) 每次遍历过程中，当nums[j] < nums[i]，意味着2者都不在其正确位置，若要得到正确排序，需要进行位置的交换，但此处不要求交换，因此将i标记为Unsorted Array的最底端，j标记为Unsorted Array的最顶端

sort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        vector<int> numsCopy(nums.begin(), nums.end());
        sort(nums.begin(), nums.end());
        int l = nums.size();
        int r = 0;
        for(int i = 0; i < nums.size(); ++i)
        {
            if(nums[i] != numsCopy[i])
            {
                l = min(i, l);
                r = max(i, r);
            }
        }
        return l == nums.size() ? 0 : r - l + 1;
    }
};

O(nlogn)

排序后比较不同处的两个端点

stack
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        stack<int> s;
        int l = nums.size();
        int r = l;
        for(auto& num : nums)
        {
            while(!s.empty() && num < s.top())
            {
                s.pop();
                l = min(static_cast<int>(s.size()), l);
            }
            s.push(num);
        }
        stack<int> s1;
        for(auto i = nums.end() - 1; i >= nums.begin(); --i)
        {
            while(!s1.empty() && *i > s1.top())
            {
                s1.pop();
                r = min(static_cast<int>(s1.size()), r);
            }
            s1.push(*i);
        }
        return l == nums.size() ? 0 : nums.size() - r - l;
    }
};
T(n):O(n) S(n):O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        int l = nums.size(), r = 0; 
        for(int i = 1; i < nums.size(); ++i)
        {
            int j = i;
            while(j > 0 && nums[i] < nums[j - 1])
            {
                --j;
                l = min(j, l);
            }
        }
        for(int i = nums.size() - 2; i >= 0; --i)
        {
            int j = i;
            while(j < nums.size() - 1 && nums[i] > nums[j + 1])
            {
                ++j;
                r = max(j, r);
            }
        }
        return l == nums.size() ? 0 : r - l + 1;
    }
};
T(n):O(n) S(n):O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        int minNum = INT_MAX, maxNum = INT_MIN;
        for(auto i = nums.begin() + 1; i != nums.end(); ++i)
        {
            if(*i < *(i - 1))
                minNum = min(minNum, *i);
        }
        for(auto i = nums.end() - 2; i >= nums.begin(); --i)
        {
            if(*i > *(i + 1))
                maxNum = max(maxNum, *i);
        }
        int l, r;
        for(l = 0; l < nums.size(); ++l)
        {
            if(nums[l] > minNum)
                break;
        }
        for(r = nums.size() - 1; r >= 0; --r)
        {
            if(nums[r] < maxNum)
                break;
        }
        return minNum == INT_MAX ? 0 : r - l + 1;
    }
};
review

将数组分为三部分NumsA, NumsB, NumsC

其中NumsA和NumsC是有序的，而NumsB是无序的

他们具有如下的规律，NumsA中的所有数字小于NumsB中的最小数字，而NumsC中的所有数字都大于NumsB中的最大数字

转换条件就是NumsB和NumsC中的最小值大于NumsA中的最大值，NumsA和NumsB中的最大值小于NumsC中的最小值 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        int right = -1, left = -1;
        int maxn = INT_MIN, minn = INT_MAX;
        int n = nums.size();
        // maxn记录NumsA和NumsB中的最大值，如果这个最大值比后面这个nums[i]大的话，说明不满足NumsA和NumsB中的最大值小于NumsC中的最小值
        // 因此需要更新right为i，表示至少这个i是肯定不满足顺序的
        // 如果都满足，就不断更新maxn为当前最大值，如果后面都是升序，那么right就不会变
        // 因为需要获取左边部分的最大值，所以需要从左向右遍历
        for(int i = 0; i < n; ++i)
        {
            if(maxn > nums[i])
                right = i;
            else
                maxn = nums[i];
        }
        // minn记录NumsB和NumsC中的最小值，如果这个最小值比前面这个nums[i]小的话，说明不满足NumsB和NumsC中的最小值大于NumsA中的最大值
        // 因此需要更新left为i，表示至少这个i是肯定不满足顺序的
        // 如果都满足，就不断更新minn为当前最小值，如果后面都是降序，那么left就不会变
        // 因为需要获取右边部分的最小值，所以需要从右向左遍历
        for(int i = n - 1; i >= 0; --i)
        {
            if(minn < nums[i])
                left = i;
            else
                minn = nums[i];
        }
        return right == -1 ? 0 : right - left + 1;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 2k Reading time ≈ 2 mins.

300. Longest Increasing Subsequence

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> heap;
        for(auto& num : nums)
        {
            auto i = std::lower_bound(heap.begin(), heap.end(), num);
            if(i == heap.end())
                heap.push_back(num);
            else
                *i = num;
        }
        return heap.size();
    }
};
不使用std::lower_bound
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> heap;
        for(auto& num : nums)
        {
            auto i = binarySearch(heap.begin(), heap.end(), num);
            if(i == heap.end())
                heap.push_back(num);
            else
                *i = num;
        }
        return heap.size();
    }
private:
    vector<int>::iterator binarySearch(vector<int>::iterator begin, vector<int>::iterator end, int num)
    {
        vector<int>::iterator it;
        int count = end - begin;
        int step;
        while(count > 0)
        {
            it = begin;
            step = count / 2;
            it += step;
            if(*it < num)
            {
                begin = ++it;
                count -= step + 1;
            }else
                count = step;
        }
        return begin;
    }
};
review
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> piles;
        for(auto& num : nums)
        {
            auto i = binarySearch(piles, 0, piles.size(), num);
            if(i != piles.size())
                piles[i] = num;
            else
                piles.push_back(num);
        }
        return piles.size();
    }
private:
    int binarySearch(vector<int>& nums, int lo, int hi, int target)
    {
        while(lo < hi)
        {
            int mid = (lo + hi) >> 1;
            if(nums[mid] < target)
                lo = mid + 1;
            else
                hi = mid;
        }
        return hi;
    }
};

视频介绍:

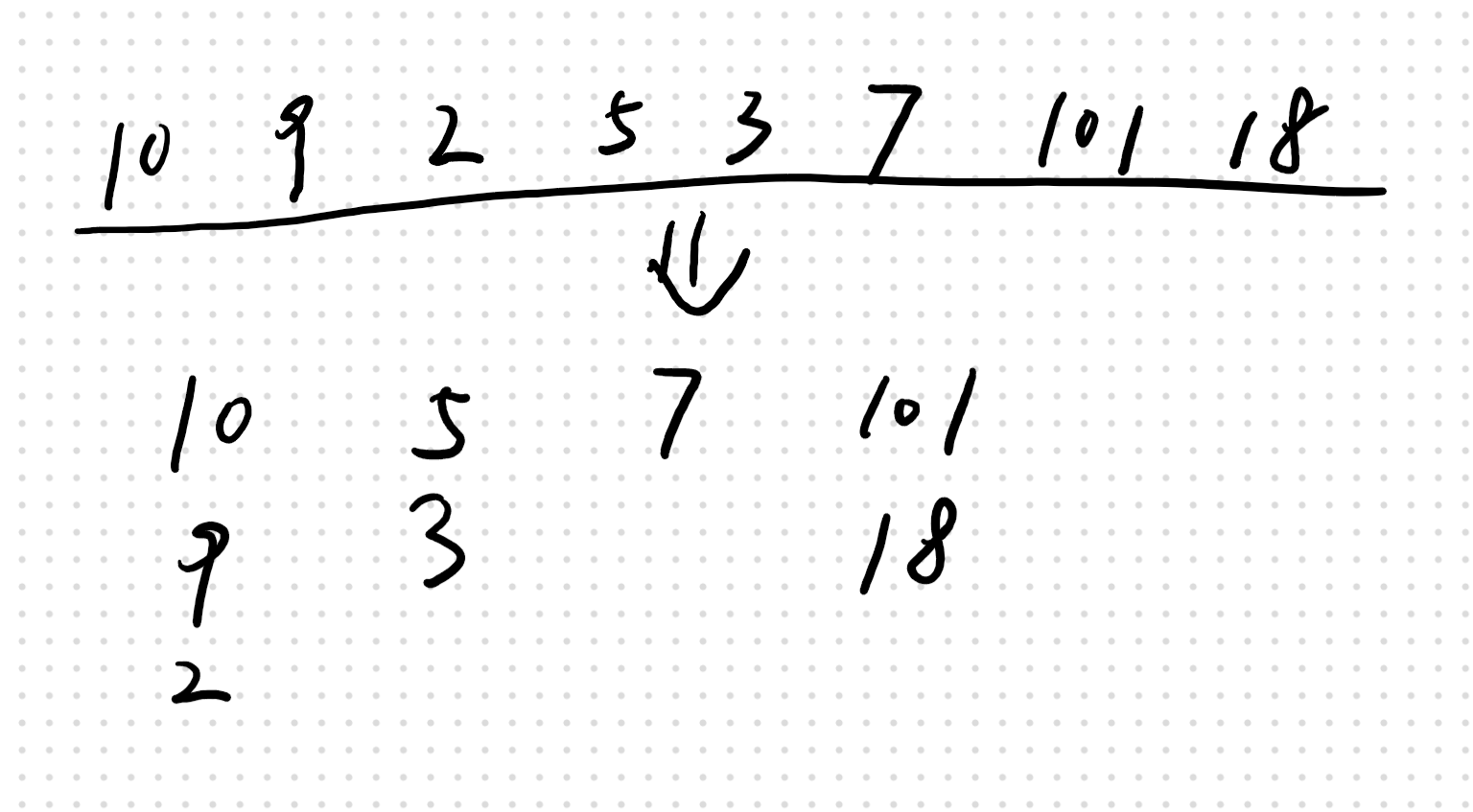1619669700668.png 如图，把所有牌分堆，从左开始寻找，一旦找到他比某个牌堆的顶端少，就放过去，以贪婪原则。

这样分出的排队数量就是里面的最长增长的串，保证这一点可以通过数学归纳法，详情见视频3:43, 直观的理解是因为：
每个排队中的顺序都是依据原数组中顺序递减的，因此，每个牌堆中最多只能取一张牌，因此增长序列长度<=牌堆数

dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int> f(n);
        int ret{ 0 };
        for(int i = 0; i < n; ++i)
        {
            int len = 1;
            for(int j = 0; j < i; ++j)
                if(nums[i] > nums[j])
                    len = max(len, f[j] + 1);
            ret = max(len, ret);
            f[i] = len;
        }
        return ret;
    }
};

引368. 最大整除子集

Posted on Edited on In Disqus:
Symbols count in article: 2k Reading time ≈ 2 mins.

138. Copy List with Random Pointer

hashmap && vector
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/

class Solution {
public:
    Node* copyRandomList(Node* head) {
        int i = 0;
        auto headTmp = head;
        Node* newHead = new Node(0);
        Node* newHeadTmp = newHead;
        
        unordered_map<Node*, int> map;
        vector<Node*> newMap;
        while(headTmp)
        {
            Node* nodeTmp = new Node(headTmp->val);
            
            newHeadTmp->next = nodeTmp;
            newHeadTmp = newHeadTmp->next;
            
            newMap.push_back(nodeTmp);
            map[headTmp] = i++;
            
            headTmp = headTmp->next;
        }
        headTmp = head;
        
        newHeadTmp = newHead;
        newHead = newHead->next;
        delete newHeadTmp;
        
        i = 0;
        while(headTmp)
        {
            if(headTmp->random)
                newMap[i]->random = newMap[map[headTmp->random]];
            else
                newMap[i]->random = nullptr;
            ++i;
            headTmp = headTmp->next;
        }
        return newHead;
    }
};

T(n) : O(n)
S(n) : O(n)

discussion中O(1) space Complexity 的方法，实际上还是O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/

class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(!head)
            return nullptr;
        Node* headTmp = head;
        while(headTmp)
        {
            Node* node = new Node(headTmp->val);
            auto next = headTmp->next;
            headTmp->next = node;
            node->next = next;
            headTmp = next;
        }
        headTmp = head;
        while(headTmp)
        {
            if(headTmp->random)
                headTmp->next->random = headTmp->random->next;
            headTmp = headTmp->next->next;
        }
        headTmp = head;
        Node* newHead = head->next;
        Node* newHeadTmp = newHead;
        while(newHeadTmp->next)
        {
            headTmp->next = headTmp->next->next;
            headTmp = headTmp->next;
            
            newHeadTmp->next = headTmp->next;
            newHeadTmp = newHeadTmp->next;
        }
        headTmp->next = headTmp->next->next;
        newHeadTmp->next = nullptr;
        return newHead;
    }
};

T(n) : O(n)
S(n) : O(n)

Posted on Edited on In Disqus:
Symbols count in article: 417 Reading time ≈ 1 mins.

560. Subarray Sum Equals K

和https://leetcode.com/problems/path-sum-iii/思路相同
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> map;
        map[0] = 1;
        int count = 0;
        int curSum = 0;
        for(auto& num : nums)
        {
            curSum += num;
            if(map.find(curSum - k) != map.end())
                count += map[curSum - k];
            map[curSum] += 1; // 之所以要后面加，是为了当k=0时候，如果前面加意味着当前位都不去，那不行啊
        }
        return count;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.8k Reading time ≈ 2 mins.

416. Partition Equal Subset Sum

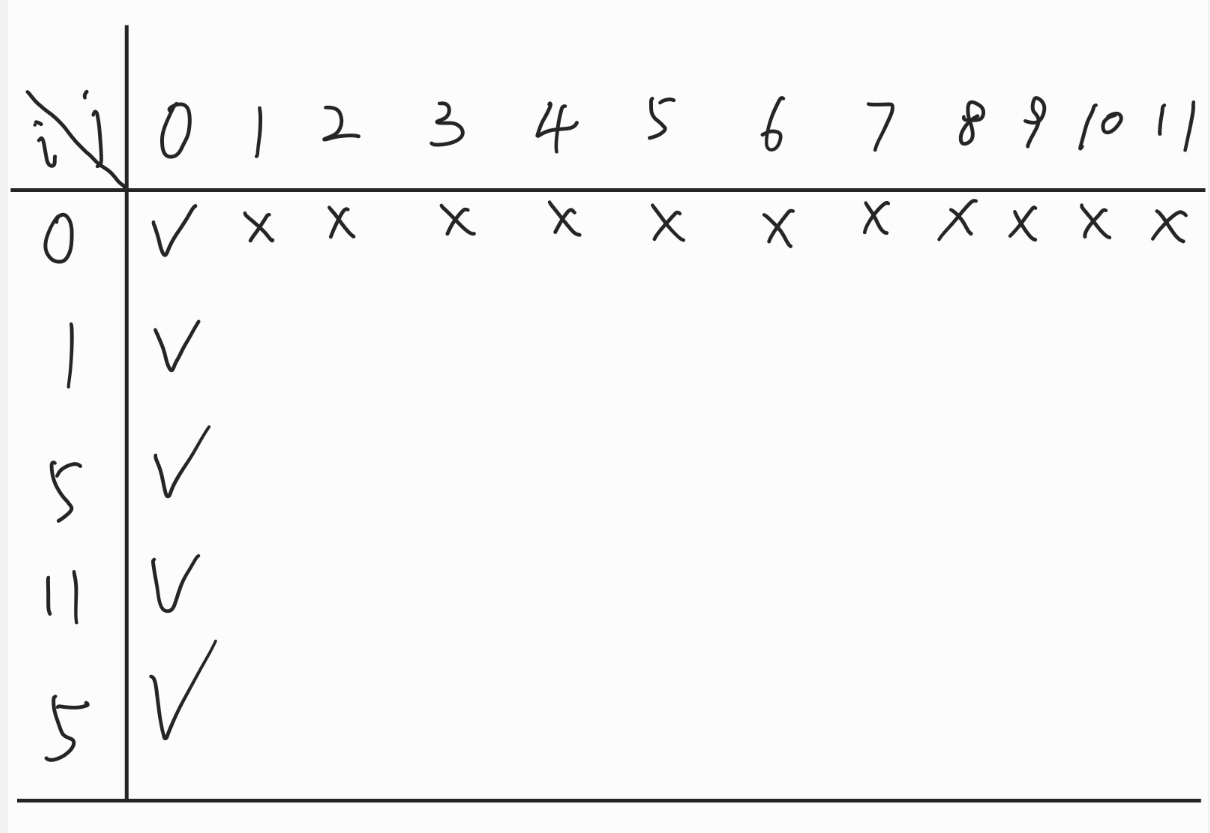
若求是否存在两个子序列相等，只需要求序列中是否存在子序列和等于总序列的一半。所以当和为奇数时候就是无效的。

转化为dp

dp[i][j]表示0~i的数字能否获得和为j，若能为true，不能为false。

对于一行的dp[i][j]来说

  1. 取当前这个nums[i]，则如果0~i-1的数字可以达到j - nums[i]和的话就是true，反之为false。也就是dp[i - 1][j - nums[i]]是否为true
  2. 不取当前这个nums[i - 1]，则如果0~i-1可以达到和为j，也就是dp[i - 1][j]是否为true。

基础情况是当没有数字时，当且仅当j为0时为true。当和为0时，对于所有数字都是true，因此只需要不取。

二维dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for(auto& num : nums)
            sum += num;
        if(sum & 1)
            return false;
        sum >>= 1;
        vector<vector<bool>> dp(nums.size() + 1, vector<bool>(sum + 1, false));
        dp[0][0] = true;
        for(int i = 1; i <= sum; ++i)
            dp[0][i] = false;
        for(int i = 1; i <= nums.size(); ++i)
            dp[i][0] = true;
        for(int i = 1; i <= nums.size(); ++i)
        {
            for(int j = 1; j <= sum; ++j)
            {
                dp[i][j] = dp[i - 1][j] || (j >= nums[i - 1] ? dp[i - 1][j - nums[i - 1]] : false);
            }
        }
        return dp.back()[sum];
    }
};
dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for(auto& num : nums)
            sum += num;
        if(sum & 1)
            return false;
        sum >>= 1;
        vector<bool> dp(sum + 1, false);
        dp[0] = true;
        for(int i = 1; i <= nums.size(); ++i)
        {
            for(int j = sum; j > 0; --j)
            {
                dp[j] = dp[j] || (j >= nums[i - 1] ? dp[j - nums[i - 1]] : false);
            }
        }
        return dp.back();
    }
};

此处从sum走是因为，i - num是一个小于 i 的值，可以保证走在后面的时候这个值还是上一行生成的结果，如果从小到大走，走到后面时就会把前面的结果刷新掉了

review

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        auto sum = accumulate(nums.begin(), nums.end(), 0);
        if(sum & 1)
            return false;
        sum /= 2;
        int m = nums.size();
        vector<bool> dp(sum + 1, false);
        dp[0] = true;
        for(int i = 0; i < m; ++i)
        {
            for(int j = sum; j >= 0; --j)
                dp[j] = dp[j] || (j >= nums[i] && dp[j - nums[i]]); 
            if(dp[sum])
                return true;
        }
        return false;
    }
};