Cinte's Leetcode Record
0%

Posted on Edited on In Disqus:
Symbols count in article: 1.5k Reading time ≈ 1 mins.

114. Flatten Binary Tree to Linked List

我越来越菜了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        stack<TreeNode*> s;
        s.push(root);
        TreeNode* cur = root;
        int i{ 0 };
        while(cur || !s.empty())
        {
            while(cur)
            {
                s.push(cur);
                cur = cur->left;
            }
            cur = s.top();
            s.pop();
            if(++i == k)
                return cur->val;
            cur = cur->right;
        }
        return 0;
    }
};

in-order 遍历就是从小到大的排序，因此只需要进行in-order遍历

中序遍历中先把最左边的加进栈，然后走一个节点的右边。当没有右树的就会进入下一个循环走到上一个树

inorder递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        int ret;
        inorder(root, ret, k);
        return ret;
    }
private:
    void inorder(TreeNode* root, int& ret, int& k)
    {
        if(!root)
            return;
        inorder(root->left, ret, k);
        if(--k == 0)
        {
            ret = root->val;
            return;
        }
        inorder(root->right, ret, k);
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.7k Reading time ≈ 2 mins.

114. Flatten Binary Tree to Linked List

我越来越菜了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 // preorder traversal 是 root -> left -> right
 // 此方法是将左子树插入到root 和 右子树中间。
class Solution {
public:
    void flatten(TreeNode* root) {
        TreeNode* now = root; // 当前节点
        while(now)
        {
            // 如果当前节点存在左子树，则需要优先遍历
            if(now->left) 
            {
                TreeNode* pre = now->left;
                // 将pre指针移到左子树的右子树的最右端
                while(pre->right)
                {
                    pre = pre->right;
                }
                // 使右子树最末端的右边只想原节点的右子树
                pre->right = now->right;
                // 将源节点的右边指向左边
                now->right = now->left;
                // 上述的操作之后，root的右子树是原来的左子树
                now->left = nullptr;
            }
            // 走到下一个节点，顺序始终是先左后右
            now = now->right;
        }
    }
};

太强了

review

和上面区别就是他留了一部分左子树给后面处理，而我就直接处理完了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        TreeNode* pt = root;
        while(pt)
        {
            if(pt->left)
            {
                auto cur = pt->left;
                TreeNode* pre;
                while(cur)
                {
                    pre = cur;
                    if(cur->right)
                        cur = cur->right;
                    else
                        cur = cur->left;
                }
                pre->right = pt->right;
                pt->right = pt->left;
                pt->left = nullptr;
            }
            pt = pt->right;
        }
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 2k Reading time ≈ 2 mins.

394. Decode String

我越来越菜了

由于括号是包裹的，后出现的左括号会匹配后面遇到的第一个右括号，所以使用堆栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    string decodeString(string s) {
        string ret = "";
        stack<string> st; // 保存遇到方括号之前的字符串
        stack<int> num; // 保存方括号前的计数
        int curNum = 0;
        for(auto& ch : s)
        {
            if(ch == '[')
            {
                st.push(ret); // 遇到方括号开端后，先压入当前字符串，当进入方括号过程中中再次遇到，就会压入先前方括号开端到此方括号之间的字符串
                num.push(curNum); // 计数值同理
                curNum = 0; // 此方括号计数已经入栈，所以开始下一轮计数
                ret = ""; // 开始计算方括号中的字符串
            }else if(ch == ']')
            {
                auto p = st.top(); // 遇见结尾，出栈，先把这个方括号之前，上一个方括号之后的字符串出栈
                st.pop();
                auto c = num.top(); // 当前方括号的计数值出栈
                num.pop();
                for(int i = 0; i < c; ++i)
                    p += ret; // 之前的加上当前括号的值，代表了前一个大括号所包含的字符串
                ret = p;
            }else if(ch <= '9' && ch >= '0')
                curNum = curNum * 10 + ch - '0';
            else
                ret += ch;
        }
        return ret;
    }
};
递归

本质上就是将堆栈方法改为了函数递归栈实现，碰到]就返回，碰到[就进去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    string decodeString(string s) {
        int index = 0;
        return helper(s, index);
    }
private:
    string helper(string& s, int& index)
    {
        string ret = "";
        int num = 0;
        while(index < s.size())
        {
            if(s[index] == ']')
                break;
            if(s[index] >= 'a' && s[index] <= 'z')
                ret += s[index++];
            else
            {
                int num = 0;
                while(s[index] >= '0' && s[index] <= '9')
                    num = num * 10 + s[index++] - '0';
                ++index;
                auto t = helper(s, index);
                while(num-- > 0)
                    ret += t;
                ++index;
            }
        }
        return ret;
    }
};

处理一个框框中的数据，框框里遇到框框就再递归

review

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    string decodeString(string s) {
        int i = 0;
        return helper(s, i, s.size());
    }
private:
    string helper(string& s, int& i, int n)
    {
        int num = 0;
        string ret;
        for(; i < n; ++i)
        {
            if(s[i] >= '0' && s[i] <= '9')
                num = num * 10 + s[i] - '0';
            else if(s[i] == ']')
                return ret;
            else if(s[i] == '[')
            {
                string inner = helper(s, ++i, n);
                if(num == 0)
                    num = 1;
                do
                    ret += inner;
                while(--num);
            }else
                ret += s[i];
        }
        return ret;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.6k Reading time ≈ 1 mins.

287. Find the Duplicate Number

很绕，由于不能改数组，这种情况废弃

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int lo = 0, hi = nums.size() - 1;
        while(lo < hi)
        {
            int mid = (lo + hi) / 2;
            if(mid + 1 <= nums[mid]) // 这里不能用不等号，因为只如果全是正确排列的话，这个一定是等号，如果mid左边出现了重复，那么mid的数会不等于mid+1，但是nums[mid] < mid + 1的情况当且仅当重复数出现在左边或本身就是重复数时才会发生。因此这种情况必然是hi=mid。而nums[mid] >= mid + 1时，如果自身是重复数，那么其余的重复数必然出现在他的右边，因为如果在左边的话，那肯定就小于了。如果自身不是，那就是nums[mid] == mid + 1的情况，也肯定在右边。
                lo = mid + 1;
            else if(mid + 1 > nums[mid])
                hi = mid;
        }
        return hi;
    }
};

T(N) : O(nlogn)

S(n) : O(1)

另一种使用二分

设cnt为数组中小于等于当前元素的元素的个数，设当前mid为target

将重复的数字看作是插入到了数组中，当插入到了比target小的数中，那么设i < target，cnt[i]必然<i，当插入到了比target大的数中，设j > target，cnt[j]必然>j，因为多了一个比他小的cnt。

如果都正常的话，在1~target-1区间中的数cnt[i]==i，target~n中的数必然>j

由此，在1~n区间内进行二分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int cnt = 0;
        int lo = 1, hi = nums.size() - 1;
        while(lo < hi)
        {
            int mid = lo + (hi - lo) / 2;
            cnt = 0;
            for(auto& num : nums)
                cnt += num <= mid ? 1 : 0;
            if(cnt <= mid)
                lo = mid + 1;
            else
                hi = mid;
        }
        return hi;
    }
};
使用cycle，有点静态链表的思想，其中的链表组成如图
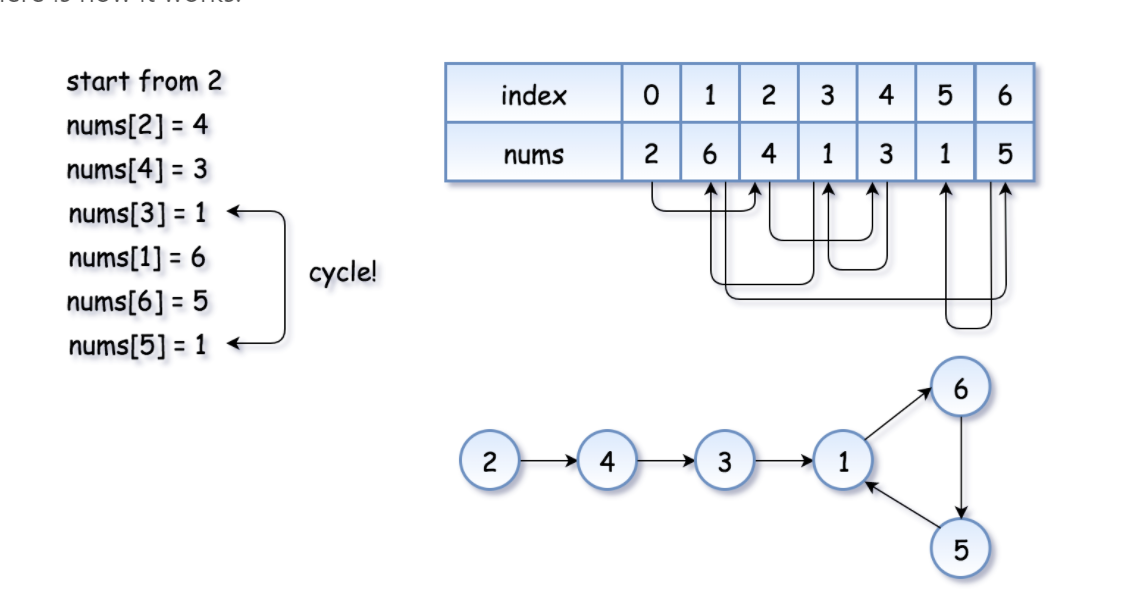
image.png

由于位于0处的数字不可能是0，所以他不可能原地跳不出去。 如果碰到一个原地跳不出去的，那就说明已经是环了

最后套用142. Linked List Cycle II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int walker = nums[0];
        int runner = nums[0];
        
        do
        {
            walker = nums[walker];
            runner = nums[nums[runner]];
        }while(walker != runner);
        
        walker = nums[0];
        while(walker != runner)
        {
            walker = nums[walker];
            runner = nums[runner];
        }
        return runner;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.5k Reading time ≈ 1 mins.

739. Daily Temperatures

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& T) {
        vector<int> next(101, INT_MAX);
        vector<int> ret(T.size(), 0);
        for(int i = T.size() - 1; i >= 0; --i)
        {
            int warmer = INT_MAX;
            for(int j = T[i] + 1; j <= 100; ++j)
            {
                if(next[j] < warmer)
                {
                    warmer = next[j];
                }
            }
            if(warmer < INT_MAX)
                ret[i] = warmer - i;
            next[T[i]] = i;
        }
        return ret;
    }
};

从后开始，对于温度为70的，接下来只会出现71~100的温度，只需要记录这些温度出现的天数，然后寻求一个最近的天数即可。由于是从后面开始更新的，所以不用怕前面的天数出来扰乱我

使用堆栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& T) {
        stack<int> s;
        vector<int> ret(T.size());
        for(int i = T.size() - 1; i >= 0; --i)
        {
            while(!s.empty() && T[i] >= T[s.top()])
                s.pop();
            ret[i] = s.empty() ? 0 : s.top() - i;
            s.push(i);
        }
        return ret;
    }
};

假设，对于位于i = 1处的天气为30度，若i = 2处的天气为50，而i = 4处的天气为30，显然，对于I = 1来说，i = 4是对他没有任何意义的，因此可以舍弃掉i = 4;
反之，若T[1] = 30, T[2] = 50, T[4] = 100, 则无法舍弃T[4] 因为若1和2之间出现一个60，则T[4]必须留着。

对于这种次序，只保留从大到小的序列，前面一个如果比后面大，后面的对于前面一个就无用了，就出栈，然后自己算完自己的后，入栈，一人就可以遮蔽后买你的所有效果

另一种堆栈 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        vector<int> ret(temperatures.size(), 0);
        stack<int> s;
        for(int i = 0; i < temperatures.size(); ++i)
        {
            while(!s.empty() && temperatures[i] > temperatures[s.top()])
            {
                auto tmp = s.top();
                ret[tmp] = i - tmp;
                s.pop();
            }
            s.push(i);
        }
        return ret;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 2.3k Reading time ≈ 2 mins.

406. Queue Reconstruction by Height

O(32n) 解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        sort(people.begin(), people.end(), [](vector<int>& p1, vector<int>& p2)
             {
                 return p1[0] > p2[0] || (p1[0] == p2[0] && p1[1] < p2[1]); 
             });
        vector<vector<int>> ret;
        for(auto& p : people)
        {
            ret.insert(ret.begin() + p[1], p);
        }
        return ret;
    }
};

先插入最高的人，最高的人组成的子序列所排列的顺序一定是由其K所决定的，当插入第二大的序列后，他不会影响第一大的序列，且仅仅由其本身和比他的序列影响，由其相对位置插入，可知，当为0时，就插到比他大的0前面，为1时，就插到比他大的1前面，比他大的那个往后移一位

结合explaination 

1
2
3
4
5
6
7
8
9
10
11
12
People are only counting (in their k-value) taller or equal-height others standing in front of them. 
So a smallest person is completely irrelevant for all taller ones. And of all smallest people, the one 
standing most in the back is even completely irrelevant for everybody 
else. Nobody is counting that person. So we can first arrange everybody else, 
ignoring that one person. And then just insert that person appropriately.
Now note that while this person is irrelevant for everybody else, 
everybody else is relevant for this person - this person counts exactly everybody in front of them. So their count-value tells you exactly the index they must be standing.

So you can first solve the sub-problem with all but that one person and then just insert that person appropriately. 
And you can solve that sub-problem the same way, first solving the sub-sub-problem with all but the last-smallest person of the subproblem. 
And so on. The base case is when you have the sub-...-sub-problem of zero people. You're then inserting the people in the reverse order, i.e., 
that overall last-smallest person in the very end and thus the first-tallest person in the very beginning. That's what the above solution does, Sorting the people from the first-tallest to the last-smallest, and inserting them one by one as appropriate.
最后一个人的位置不会影响前面的人，但前面人的位置将影响到最后一个人，因此最后一个人的k必定表示其绝对位置，将其划分为一堆的子问题，每个子问题在解决时都先忽略子问题中最小的的那个数，那个数在所有其他数排列完后再插入那个绝对的位置。 依此，则从最大数开始排起，后面插入的数对于先前的序列来说必定是插入其的K位置，不断扩大子问题，往复，直到整个序列往复。最小的数插入到其的K位置。

中心思想：最小的数的k必定表示其在结果中的绝对位置，抛开这个最小的数，生成一个子问题。再抛开子问题中最小的数，生成一个子-子问题......

针对[[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]问题

  1. 先解决最后一个子问题，也就是只有[7,0],[7,1]的问题，此时他们的k表示他们的绝对位置，由此排列即可。
  2. 往上走，当问题变成[7,0],[7,1],[6,1]时，很显然[6,1]对[7,0],[7,1]不会有任何干扰，但[7,0],[7,1]对他具有干扰， 因为此时他最小，所以所有人和他相关，最小的数字的k必然表示他的绝对位置，前面有一个比他大，所以插到第一个的后面，也就是第二个的前面。所以直接把他插入到1的位置上，这时候序列就是[7,0],[6,1], [7,1]
  3. 继续，根据上面的逻辑，每一步都把这个数直接插到当前子问题的他所对应的绝对位置上。由此得解。

Posted on Edited on In Disqus:
Symbols count in article: 812 Reading time ≈ 1 mins.

338. Counting Bits

O(32n) 解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> countBits(int num) {
        vector<int> ret;
        for(int i = 0; i <= num; ++i)
        {
            int cur = i;
            int count = 0;
            // 10进制转2进制，每次共32bit
            while(cur)
            {
                int j = cur % 2;
                if(j == 1)
                    ++count;
                cur /= 2;
            }
            ret.push_back(count);
        }
        return ret;
    }
};
使用库
1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    vector<int> countBits(int num) {
        vector<int> ret;
        for(int i = 0; i <= num; ++i)
        {
            ret.push_back(__builtin_popcount(i));
        }
        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    vector<int> countBits(int num) {
        vector<int> ret(num + 1);
        for(int i = 0; i <= num; ++i)
        {
            ret[i] = ret[i >> 1] + (i & 1); // 右移相当于取出了除了最后一位的所有值，如果最后一位为1就加一，最后一位为0，那就和右移后的一样
        }
        return ret;
    }
};

右移加上最后一位，类似动态规划的思想

Posted on Edited on In Disqus:
Symbols count in article: 547 Reading time ≈ 1 mins.

763. Partition Labels

我好菜
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> partitionLabels(string S) {
        int c[26];
        vector<int> ret;
        for(int i = 0; i < S.size(); ++i)
        {
            c[S[i] - 'a'] = i; // 记录每个元素最后出现的位置
        }
        int anchor = 0;
        int last = 0;
        for(int i = 0; i < S.size(); ++i)
        {
            last = max(last, c[S[i] - 'a']); // 计算之前子串中出现的字母的最后的位置
            if(i == last) // 如果这个条件成立了，表示当前子串(anchor - i)中的所有字母都只出现过了一次，并且之后不会再出现了，所以开始i计算并保存结果。
            {
                ret.push_back(last + 1 - anchor);
                anchor = last + 1;
            }
        }
        return ret;
        
    }
};

每走到一步就判断他的最后一位，差不多就寻求一个最大区间

Posted on Edited on In Disqus:
Symbols count in article: 1.4k Reading time ≈ 1 mins.

283. Move Zeroes

两步： 1. 保持原顺序 2. 零在最后面

总体思路
先实现1后实现2，需要认识到如下之点

The 2 requirements of the question are:

  1. Move all the 0's to the end of array.

  2. All the non-zero elements must retain their original order.

It's good to realize here that both the requirements are mutually exclusive, i.e., you can solve the individual sub-problems and then combine them for the final solution.

很直观的方法，但有时也是非常好用的办法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int sz = nums.size();
        int numOfZero = 0;
        for(auto& num : nums)
        {
            numOfZero += (num == 0);
        }
        vector<int> ans;
        for(auto& num :nums)
        {
            if(num != 0)
                ans.push_back(num);
        }
        
        for(int i = 0; i < sz - numOfZero; ++i)
        {
            nums[i] = ans[i];
        }
        fill(nums.begin() + sz - numOfZero, nums.end(), 0);
    }
};

T(n) : O(n)
S(n) : O(n)

对上述方法优化空间占用
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int noZeroIndex = 0;
        for(auto& num :nums)
        {
            if(num != 0)
                nums[noZeroIndex++] = num;
        }
        fill(nums.begin() + noZeroIndex, nums.end(), 0);
    }
};

T(n) : O(n) S(n) : O(1)

再优化，由于上面需要执行完N次操作，还可以优化
1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int noZeroIndex = 0;
        for(auto& num :nums)
        {
            if(num != 0)
                swap(nums[noZeroIndex++], num);
        }
    }
};

T(n) : O(n)
S(n) : O(1)

这里仅需要执行非0的个数

由于noZeroIndex和num不同时，noZeroIndex指向的必定是0元素，这时与num进行交换就可以将0元素移动到后头，依次往复，所有的0都会跑到后面去

因为如果是0，noZeroIndex就不会加，就会留着，如果相同，那就是自己加自己。

Posted on Edited on In Disqus:
Symbols count in article: 1.5k Reading time ≈ 1 mins.

234. Palindrome Linked List

很慢的two Point
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    bool isPalindrome(ListNode* head) {
        ListNode* walker = head;
        ListNode* runner = head;
        stack<int> s;
        while(walker)
        {
            if(runner)
            {
                if(runner->next)
                {
                    s.push(walker->val);
                    runner = runner->next->next;
                }else
                    runner = nullptr;
                
            }else
            {
                if(s.top() != walker->val)
                    return false;
                s.pop();
            }
            walker = walker->next;
        }
        return true;
    }
};
使用链表反转
two point 法2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    bool isPalindrome(ListNode* head) {
        ListNode* rev = nullptr;
        ListNode* runner = head;
        ListNode* walker = head;
        while(runner && runner->next)
        {
            runner = runner->next->next;
            ListNode *tmp = rev;
            rev = walker;
            walker = walker->next;
            rev->next = tmp;
        }
        if(runner)
            walker = walker->next;
        while(rev && rev->val == walker->val)
        {
            rev = rev->next;
            walker = walker->next;
        }
        return rev ? false : true;
    }
};