Cinte's Leetcode Record
0%

Posted on Edited on In Disqus:
Symbols count in article: 1.7k Reading time ≈ 2 mins.

543. Diameter of Binary Tree

遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int diameterOfBinaryTree(TreeNode* root) {
        if(!root) return 0;
        queue<TreeNode*> q;
        q.push(root);
        int ret = 0;
        while(!q.empty())
        {
            auto p = q.front();
            q.pop();
            int dL = 0, dR = 0;
            if(p->left)
            {
                q.push(p->left);
                maxDepth(p->left, dL, 0);
            }
            if(p->right)
            {
                q.push(p->right);
                maxDepth(p->right, dR, 0);
            }
            ret = max(ret, dL + dR);
        }
        return ret;
    }
private:
    void maxDepth(TreeNode* root, int& depth, int tmp)
    {
        if(!root)
            return;
        ++tmp;
        depth = max(tmp, depth);
        maxDepth(root->left, depth, tmp);
        maxDepth(root->right, depth, tmp);
        --tmp;
    }
};
顺路计算完所有的点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int diameterOfBinaryTree(TreeNode* root) {
        int maxDepth = 0;
        longest(root, maxDepth);
        return maxDepth;
    }
private:
    int longest(TreeNode* root, int &maxDepth)
    {
        if(!root) return 0;
        
        int left = longest(root->left, maxDepth);
        int right = longest(root->right, maxDepth);
        
        maxDepth = max(maxDepth, left + right);
        return max(left, right) + 1;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.9k Reading time ≈ 2 mins.

215. Kth Largest Element in an Array

?直接用sort
1
2
3
4
5
6
7
class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end());
        return *(nums.end() - k);
    }
};

T(n) : O(nlogn)

手生了，写一下快速排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        quickSort(nums, 0, nums.size() - 1);
        return *(nums.end() - k);
    }
private:
    void quickSort(vector<int>& nums, int lo, int hi)
    {
        if(lo >= hi) return;
        auto j = pa(nums, lo, hi);
        quickSort(nums, lo, j - 1);
        quickSort(nums, j + 1, hi);
    }
    
    int pa(vector<int>& nums, int lo, int hi)
    {
        int v = nums[lo];
        int i{ lo };
        int j { hi + 1};
        while(1)
        {
            while(i < hi && nums[++i] < v) {}
            while(j > lo && nums[--j] > v) {}
            if(i >= j) break;
            swap(nums[i], nums[j]);
        }
        swap(nums[j], nums[lo]);
        return j;
    }
};
使用优先级队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        priority_queue<int> pq;
        for(auto& num : nums)
        {
            pq.push(num);
            
            if(pq.size() > nums.size() - k + 1)
                pq.pop();
        }
        return pq.top();
    }
};

T(n) : O(nlogn)
S(n) : O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        k = nums.size() - k;
        int lo{ 0 };
        int hi = nums.size() - 1;
        while(lo < hi)
        {
            auto j = pa(nums, lo, hi);
            if(j > k)
                hi = j - 1;
            else if (j < k)
                lo = j + 1;
            else
                break;
        }
        return nums[k];
    }
private:
    int pa(vector<int>& nums, int lo, int hi)
    {
        int v = nums[lo];
        int i{ lo };
        int j { hi + 1};
        while(1)
        {
            while(i < hi && nums[++i] < v) {}
            while(j > lo && nums[--j] > v) {}
            if(i >= j) break;
            swap(nums[i], nums[j]);
        }
        swap(nums[j], nums[lo]);
        return j;
    }
};

最好的情况下时只进行一次partition， 为O(n)
最坏的情况是对于每个元素都进行partition 为O(n^2)

将原数组进行洗牌后可以保证O(n)

Posted on Edited on In Disqus:
Symbols count in article: 2.3k Reading time ≈ 2 mins.

200. Number of Islands

DFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int count{ 0 };
        for(int i = 0; i < grid.size(); ++i)
        {
            for(int j = 0; j < grid[0].size(); ++j)
            {
                if(grid[i][j] == '1')
                {
                    dfs(grid, i, j);
                    ++count;
                }
            }
        }
        return count;
    }
    void dfs(vector<vector<char>>& grid, int i, int j)
    {
        if(i < 0 || j < 0 || i >= grid.size() || j >= grid[0].size() || grid[i][j] != '1') // 这里不能用grid[i][j] == '0'，因为会导致dfs过程无限走
            return;
        grid[i][j] = '.';
        dfs(grid, i + 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i - 1, j);
        dfs(grid, i, j - 1);
    }
};

深度优先遍历，当遇到一块陆地后，向周围遍历，遍历过的土地做上标记防止重复遍历，当遍历完一整块岛后，返回，计数加一

使用并查集

对discuss中的代码加以批注

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int[][] distance = {{1,0},{-1,0},{0,1},{0,-1}}; // 4个方向
public int numIslands(char[][] grid) {  
    if (grid == null || grid.length == 0 || grid[0].length == 0)  {
        return 0;  
    }
    UnionFind uf = new UnionFind(grid);  
    int rows = grid.length;  
    int cols = grid[0].length;  
    for (int i = 0; i < rows; i++) {  
        for (int j = 0; j < cols; j++) {  
            if (grid[i][j] == '1') {  // 当遇上陆地
                for (int[] d : distance) { // 陆地的4个方向进行遍历
                    int x = i + d[0]; 
                    int y = j + d[1];
                    if (x >= 0 && x < rows && y >= 0 && y < cols && grid[x][y] == '1') { // 当且仅当是陆地时进入循环
                        int id1 = i*cols+j; // 当前陆地的id ，展开成1维表示
                        int id2 = x*cols+y; // 周围陆地的id，同样是展开成一维
                        uf.union(id1, id2); // 进行并查，具体见UnionFind CLASS
                    }  
                }  
            }  
        }  
    }  
    return uf.count;  
}

Union Find:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class UnionFind {
    int[] father;  
    int m, n;
    int count = 0;
    UnionFind(char[][] grid) {  
        m = grid.length;  
        n = grid[0].length;  
        father = new int[m*n];  
        for (int i = 0; i < m; i++) {  
            for (int j = 0; j < n; j++) {  
                if (grid[i][j] == '1') {
                    int id = i * n + j;
                    father[id] = id; // 对每一个陆地初始化，初始化后，每个陆地都各自分为一类
                    count++; // 在归并之前，总数
                }
            }  
        }  
    }
    public void union(int node1, int node2) {  
        int find1 = find(node1); // 查找node 1 和 node 2属于哪一类
        int find2 = find(node2);
        if(find1 != find2) {
            father[find1] = find2; // 由于二者是邻接的陆地，因此当二者属于的类不同时，将其合并
            count--; // 2块陆地合并，计数减一
        }
    }
    // 递归查找所属的类，直到查找到其所属的最顶端类
    public int find (int node) {
        if (father[node] == node) {  
            return node;
        }
        father[node] = find(father[node]);  
        return father[node];
    }
}

Posted on Edited on In Disqus:
Symbols count in article: 2.1k Reading time ≈ 2 mins.

152. Maximum Product Subarray

仿kadane算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int maxSoFar = nums[0];
        
        int maxEndHere = nums[0];
        int minEndHere = nums[0];
        for(auto i = nums.begin() + 1; i != nums.end(); ++i)
        {
            int num = *i;
            if(num < 0)
                swap(maxEndHere, minEndHere); // 如果num<0，那么乘了之后，他们势必会翻转，max如果是大的，乘后就会变小
            
            maxEndHere = max(num, maxEndHere * num); // 假如还不如现在的大，那么你也没用啊，我不如前面的不乘了
            minEndHere = min(num, minEndHere * num); //
            
            maxSoFar = max(maxEndHere, maxSoFar);
        }
        return maxSoFar;
    }
};
另一种思路
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int maxNum{ nums[0] };
        int product{ 1 };
        for(auto i = nums.begin(); i != nums.end(); ++i)
        {
            maxNum = max(maxNum, product *= *i);
            if(!*i) product = 1;
        }
        product = 1;
        for(auto i = nums.end() - 1; i != nums.begin(); --i)
        {
            maxNum = max(maxNum, product *= *i);
            if(!*i) product = 1;
        }
        return maxNum;
    }
};
review
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int ret = nums[0];
        int curLR = 1;
        int curRL = 1;
        for(int i = 0, j = nums.size() - 1; i < nums.size(); ++i, --j)
        {
            ret = max(ret, max(curLR *= nums[i], curRL *= nums[j]));
            if(nums[i] == 0)
                curLR = 1;
            if(nums[j] == 0)
                curRL = 1;
        }
        return ret;
    }
};

当负数的个数为偶数时，全乘起来就是最大，为奇数时，需要抛弃一个
每次的乘法，最大的乘积受到最后一个负数的限制

review
当负数个数为偶数且中间没有0，那么无论左到右还是右到左都会遍历到。

抛开此外，可以观察到分界线为0，每一块被0分开的没0区域都表示一个乘积，当这一个区域没有负数或者负数个数为偶数，那么无论左到右还是右到左都会遍历到。当为奇数，那么以其中一个负数为分界线将分成左右2块为偶的区域，由此需要左到右和右到左遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int ret = INT_MIN;
        int begin = 0;
        int n = nums.size();
        for(int i = 0; i < n; ++i)
        {
            if(nums[i] == 0)
            {
                ret = max(ret, helper(nums, begin, i));
                begin = i + 1;
            }
        }
        ret = max(ret, helper(nums, begin, n));
        if(begin != 0 && ret < 0)
            ret = 0;
        return ret;
    }
private:
    int helper(vector<int>& nums, int start, int end)
    {
        int ret = INT_MIN;
        int cur = 1;
        for(int i = start; i < end; ++i)
        {
            cur *= nums[i];
            ret = max(ret, cur);
        }

        cur = 1;
        for(int i = end - 1; i >= start; --i)
        {
            cur *= nums[i];
            ret = max(ret, cur);
        }
        return ret;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.1k Reading time ≈ 1 mins.

448. Find All Numbers Disappeared in an Array

抄的discussion

使用原数列中的坐标是否为负来表征当前坐标所代表的值是否存在。由此使得S(n) = O(n)

聪明啊！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> findDisappearedNumbers(vector<int>& nums) {
        for(int i = 0; i < nums.size(); ++i)
        {
            // 下述操作也类似一个哈希表
            int m = abs(nums[i]) - 1; // 当前的数字，对应的角标，由于可能之前被操作为负的，所以要绝对值
            nums[m] = nums[m] > 0 ? -nums[m] : nums[m];  // 角标对应过去的为负，表示那个被记录到了
        }
        vector<int> ret;
        for(int i = 0; i < nums.size(); ++i)
        {
            if(nums[i] > 0)
                ret.push_back(i + 1);
        }
        return ret;
    }
};
review
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<int> findDisappearedNumbers(vector<int>& nums) {
        vector<int> ret;
        int n = nums.size() + 1;
        for(int i = 0; i < n - 1; ++i)
            while(i + 1 != nums[i] && nums[i] != nums[nums[i] - 1])
                swap(nums[i], nums[nums[i] - 1]);
        for(int i = 1; i < n; ++i)
            if(i != nums[i - 1])
                ret.push_back(i);
        return ret;
    }
};
review2
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    vector<int> findDisappearedNumbers(vector<int>& nums) {
        vector<int> ret;
        int n = nums.size() + 1;
        for(auto num : nums)
            nums[(num - 1) % n] += n;
        for(int i = 1; i < n; ++i)
            if(nums[i - 1] <= n)
                ret.push_back(i);
        return ret;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 2k Reading time ≈ 2 mins.

160. Intersection of Two Linked Lists

最直接法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        unordered_set<ListNode*> set;
        while(headA)
        {
            set.insert(headA);
            headA = headA->next;   
        }
        
        while(headB)
        {
            if(set.find(headB) != set.end())
                return headB;
            headB = headB->next;
        }
        return nullptr;
    }
};
预先求差
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        int lenA{ 0 };
        int lenB{ 0 };
        
        ListNode* a = headA;
        ListNode* b = headB;
        
        while(a)
        {
            ++lenA;
            a = a->next;
        }
        while(b)
        {
            ++lenB;
            b = b->next;
        }
        if(lenA < lenB)
        {
            for(int i = 0; i < lenB - lenA; ++i)
                headB = headB->next;
        }else
        {
            for(int i = 0; i < lenA - lenB; ++i)
                headA = headA->next;
        }
        
        while(headA && headB)
        {
            if(headA == headB)
                return headA;
            headA = headA->next;
            headB = headB->next;
        }
        
        return nullptr;
    }
};
2次迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode *a = headA;
        ListNode *b = headB;
        
        while(a != b)
        {
            a = a == nullptr ? headB : a->next;
            b = b == nullptr ? headA : b->next;
        }
        return a;
    }
};

他们第一次跑会有一个长度的差，短的先跑到终点后，到长的端点。当长的指针跑到终点后，回到短的端点。此时先前一个刚好跑了他们的距离差，这是他们在距离上是处于同一个起点的。

设短的到交点距离x，长的到交点距离y，公共部分距离为z，则如果要求交点，那么让他们走到交点的路程一致即可，则让短的走到头后跳到长，长的走到头后跳到短，最后对于短头来说x+y+z,长头也是x+y+z，刚好在交点相交。

review

如果没交点，第二轮时候他们肯定一同走到尾巴。长的比短的多出来的步数，由于短的先走到头，然后比长的走到短头会刚好多走这么几步，于是就处于同意起跑线。

具体见discussion中的评论第一条

Posted on Edited on In Disqus:
Symbols count in article: 1.7k Reading time ≈ 2 mins.

142. Linked List Cycle II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        unordered_set<ListNode*> set;
        int i = 0;
        while(head)
        {
            if(!(set.emplace(head).second))
            {
                return head;
            }
            head = head->next;
        }
        return nullptr;
    }
};

T(n) : O(n)
S(n) : O(n)

使用linked cycle中的two point 方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(!head) return nullptr;
        ListNode* walker = head;
        ListNode* runner = head;
        
        bool isMeet = false;
        while(runner->next && runner->next->next)
        {
            walker = walker->next;
            runner = runner->next->next;
            if(walker == runner)
            {
                isMeet = true;
                break;
            }
        }
        
        if(isMeet)
        {
            walker = head;
            while(walker != runner)
            {
                walker = walker->next;
                runner = runner->next;
            }
            return runner;
        }
        return nullptr;
    }
};

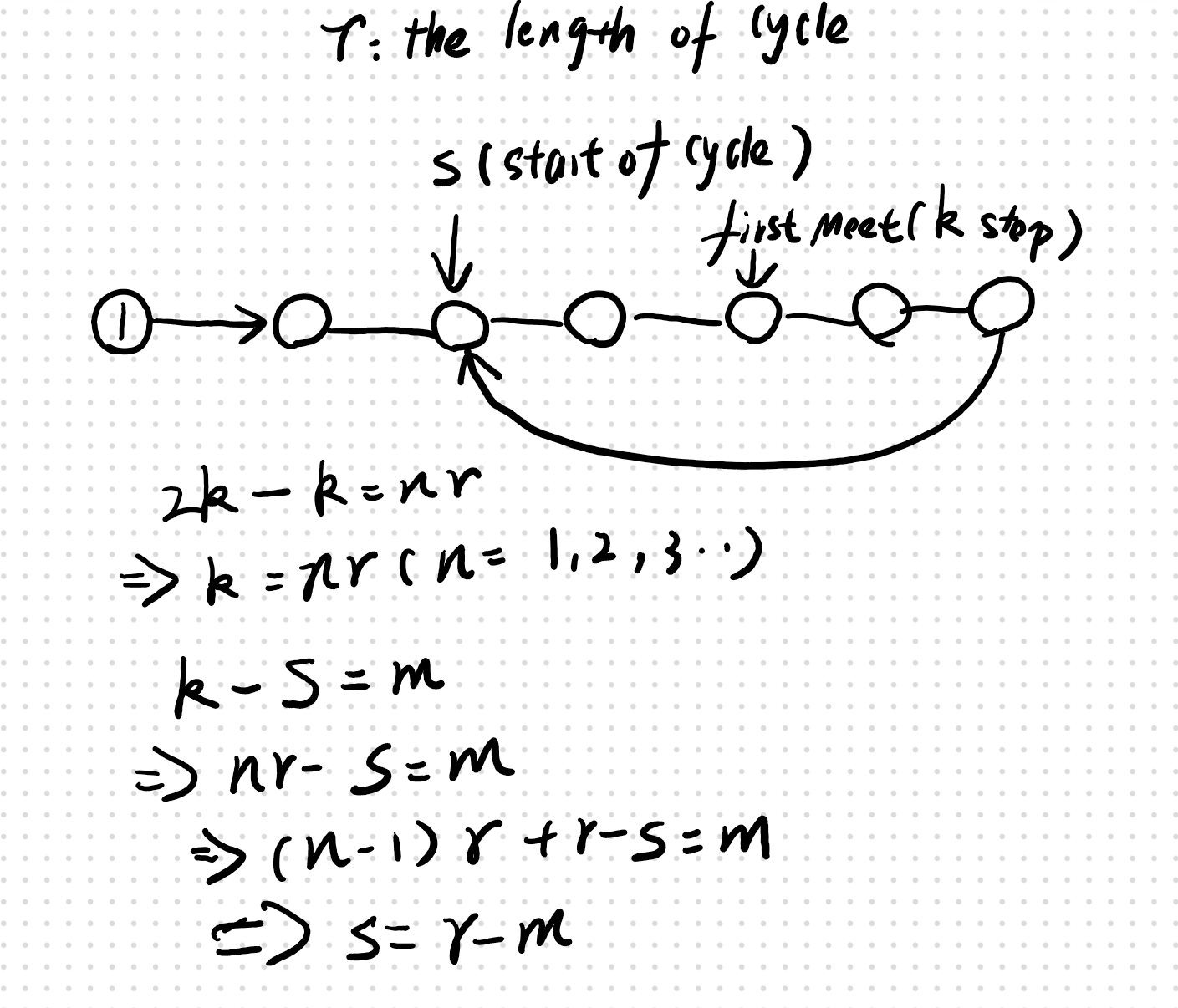image.png 即当一个点从第一次遇见的点开始，走r-m步，走到环的起始点时，另一个点刚好从起点走到环的起始点

针对最后取为1的修订 

1
Smart solution. But replacing all "wake" to "walk" in your words makes me feel better :) Another minor point is you can't just "here we takes n = 1" even it doesn't affect the last result. It still should read as s=nr-m. That means the 1st pointer starts from beginning of the list while the 2nd pointer starts from meet point, they will meet in the cycle point but the 2nd pointer walked n times of the cycle.
第二次循环时候，runner是走了r2-2r1(设为n)圈，这个数字为正即可，因为不管他多走几圈都影响不了结果。而r2是runner走的圈数，r1是walker走的圈数。

k为步数，s为起点到环起点的距离，m为圈长 r2 = (2k - s) / m，而r1 = (k - s) / m，则r2 / r1 = 2 + s/k+s，所以r2 - 2r1 = s / k + s必定为正数

Posted on Edited on In Disqus:
Symbols count in article: 1.3k Reading time ≈ 1 mins.

105. Construct Binary Tree from Preorder and Inorder Traversal

太难了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int index = 0;
        for(int i = 0; i < inorder.size(); ++i)
        {
            map[inorder[i]] = i;
        }
        return tree(preorder, 0, preorder.size() - 1, index);
    }
private:
    unordered_map<int, int> map;
    TreeNode* tree(vector<int>& preorder, int left, int right, int& index)
    {
        if(left > right)
            return nullptr;
        
        int val = preorder[index++];
        TreeNode* root = new TreeNode(val);
        root->left = tree(preorder, left, map[val] - 1, index);
        root->right = tree(preorder, map[val] + 1, right, index);
        
        return root;
    }
};

每个在preorder中的点在inorder中的左边都是左树，右边是右树

The two key observations are:

  1. Preorder traversal follows Root -> Left -> Right, therefore, given the preorder array preorder, we have easy access to the root which is preorder[0].

  2. Inorder traversal follows Left -> Root -> Right, therefore if we know the position of Root, we can recursively split the entire array into two subtrees.

Posted on Edited on In Disqus:
Symbols count in article: 1.7k Reading time ≈ 2 mins.

102. Binary Tree Level Order Traversal

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        if(!root) return {};
        vector<vector<int>> ret;
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty())
        {
            vector<int> tmp;
            for(int i = 0, n = q.size(); i < n; ++i)
            {
                auto p = q.front();
                q.pop();
                tmp.push_back(p->val);
                if(p->left)
                    q.push(p->left);
                if(p->right)
                    q.push(p->right);
            }
            ret.push_back(tmp);
        }
        return ret;
    }
};
image.png

还有使用递归，传入层数，对每一层的vector容器加入

review 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        if(!root)
            return {};
        vector<vector<int>> ret;
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty())
        {
            ret.emplace_back();
            for(int i = 0, sz = q.size(); i < sz; ++i)
            {
                auto p = q.front();
                q.pop();
                ret.back().push_back(p->val);
                if(p->left)
                    q.push(p->left);
                if(p->right)
                    q.push(p->right);
            }
        }
        return ret;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 2.3k Reading time ≈ 2 mins.

111. Minimum Depth of Binary Tree

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(!root) return 0;
        int depth{ INT_MAX };
        int tmp{ 1 };
        backTrack(root, depth, tmp);
        return depth;
    }
private:
    void backTrack(TreeNode* root, int& depth, int& tmp)
    {
        if(!root) return;
        if(!root->left && !root->right)
        {
            depth = min(depth, tmp);
            return;
        }
        ++tmp;
        backTrack(root->left, depth, tmp);
        backTrack(root->right, depth, tmp);
        --tmp;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(!root)
            return 0;
        if(!root->left)
            return minDepth(root->right) + 1; // 针对不是叶子节点的情况，不能因为当前是根而干扰结果
        if(!root->right)
            return minDepth(root->left) + 1; // 针对不是叶子节点的情况，不能因为当前是根而干扰结果
        return min(minDepth(root->left), minDepth(root->right)) + 1; // 如果当前是子树的根节点，那么会导致结果终止于这个根。所以上面2个if是保证在当前节点不是叶子节点情况下继续往下走。
    }
};
BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(!root) return 0;
        queue<TreeNode*> q;
        q.push(root);
        int depth{ 0 };
        while(!q.empty())
        {
            ++depth;
            auto sz = q.size();
            for(size_t i = 0; i < sz; ++i)
            {
                auto p = q.front();
                q.pop();
                if(p->left)
                    q.push(p->left);
                if(p->right)
                    q.push(p->right);
                if(!p->left && !p->right)
                    return depth;
            }
        }
        return depth;
    }
};