Cinte's Leetcode Record
0%

Posted on Edited on In Disqus:
Symbols count in article: 1.5k Reading time ≈ 1 mins.

47. Permutations II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<vector<int>> ret;
        sort(nums.begin(), nums.end());
        int num[8]{ 0 };
        vector<int> temp;
        backTrack(ret, nums, temp , num);
        return ret;
    }
private:
    void backTrack(vector<vector<int>>& ret, const vector<int>& nums, vector<int>& temp, int* num)
    {
        if(temp.size() == nums.size())
            ret.push_back(temp);
        for(size_t i = 0; i < nums.size(); ++i)
        {
            if(num[i]) continue;
            temp.push_back(nums[i]);
            num[i] = 1;
            backTrack(ret, nums, temp, num);
            temp.pop_back();
            num[i] = 0;
            while(i + 1 < nums.size() && nums[i] == nums[i + 1]) // 重点。从重复串的第一个元素搜索已经可以获得获得重复串的全排列结果了，所以防止后面重复得到，就跳过。也就是说，重复字符串的元素只会顺位取而不会掉头。也就是说，如果有重复的，那么搜索起点一样，肯定会重复，所以要剔除
            // 补充：他无法掉头取导致了如果他们在结果中连续，就必然只有一种排列方式。如果他们在结果被其他数字隔开来，那么必然隔开来的每段中的连续部分必然唯一，而且所有隔开来的段也必然唯一，因为如果要去后面的和前面相同的段的话，前面的段必然是已经使用过了，如果没使用，就说明被回溯了，就说明接下来的数字已经跳过了当前重复数字。
                ++i;
        }
    }
};

Another BackTrack

swap
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<string> permutation(string S) {
        backTrack(S, 0);
        return ret;
    }
private:
    vector<string> ret;
    void backTrack(string &s, int index)
    {
        if(index >= s.size())
        {
            ret.push_back(s);
            return;
        }
        // 对于后面的位来说，这个位不取重复值，就保证了不会重复结果
        unordered_set<char> memo;
        for(int i = index; i < s.size(); ++i)
        {
            if(memo.count(s[i])) 
                continue;
            memo.insert(s[i]);
            swap(s[i], s[index]);
            backTrack(s, index + 1);
            swap(s[i], s[index]);
        }
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.4k Reading time ≈ 1 mins.

46. Permutations

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> ret;
        vector<int> temp;
        int num [6]{ 0 };
        backTrack(nums, ret, temp, num);
        return ret;
    }
private:
    void backTrack(vector<int>& nums, vector<vector<int>>& ret, vector<int>& temp, int* num)
    {
        if(temp.size() == nums.size())
            ret.push_back(temp);
        for(size_t i = 0; i < nums.size(); ++i)
        {
            if(num[i]) continue;
            num[i] = 1;
            temp.push_back(nums[i]);
            backTrack(nums, ret, temp, num);
            temp.pop_back();
            num[i] = 0;
        }
    }
};

去除visited数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> ret;
        backTrack(nums, ret, nums.size(), 0);
        return ret;
    }
private:
    void backTrack(vector<int>& nums, vector<vector<int>>& ret, int length, int index)
    {
        if(index == length)
        {
            ret.push_back(nums);
            return;
        }
        for(int i = index; i < length; ++i) // 这里必须是index而不是index+1，因为index表示这个位置可以保留不动
        {
            // 将后面的数换过来，表示这个位固定为后面换过来的那个数，index之后的数都属于候选池，这样子的话每一位都可以具备所有选择。
            // 对于后面的位来说，他具备获得前面位的能力，因为前面位换到这个位是它可以保持i==index，就获得了前面那个数。
            // 最终的结果就是每一位都具备获得所有数字的能力
            swap(nums[index], nums[i]); 
            backTrack(nums, ret, length, index + 1);
            swap(nums[index], nums[i]);
        }
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 2.3k Reading time ≈ 2 mins.

37. Sudoku Solver

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
public:
    void solveSudoku(vector<vector<char>>& board) {
        for(size_t i = 0; i < 9; ++i)
        {
            for(size_t j = 0; j < 9; ++j)
            {
                auto& num = board[i][j];
                if(num != '.')
                {
                    col[num - 49][j] += 1;
                    row[i][num - 49] += 1;
                    block[i / 3][j / 3][num - 49] += 1;
                }
            }
        }
        solve(board, 0, 0);
        
    }
    
private:
    int col[9][9]{0};
    int row[9][9]{0};
    int block[3][3][9]{0};
    bool valid(size_t i, size_t j, int target)
    {
        if(col[target][j] || row[i][target] || block[i / 3 ][j /3][target])
            return false;
        else
            return true;
    }
    bool solve(vector<vector<char>>& board, int i, int j)
    {
        if(i == 9) return true;
        if(j == 9)
            return solve(board, i + 1, 0);
        if(board[i][j] != '.') 
            return solve(board, i, j + 1);
        
        for(char c = '1'; c <= '9'; ++c)
        {
            auto& num = board[i][j];
            if(valid(i, j, c - 49))
            {
                num = c;
                col[num - 49][j] = row[i][num - 49] = block[i / 3 ][j /3][num - 49] = 1;
                if(solve(board, i, j + 1))
                    return true;
                col[num - 49][j] = row[i][num - 49] = block[i / 3 ][j /3][num - 49] = 0;
                num = '.';
            }
        }
        return false;
    }
};

T(n) : O(N)

也是一个回溯的问题，但与combined sum不同的是这个回溯只得使用return 来作为停止条件，而combined sum中则以添加到vector中为结束。

review
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
    void solveSudoku(vector<vector<char>>& board) {
        for(int i = 0; i < 9; ++i)
            for(int j = 0; j < 9; ++j)
            {
                if(board[i][j] != '.')
                {
                    int num = board[i][j] - '0' - 1;
                    cols[j][num] = 1;
                    rows[i][num] = 1;
                    blocks[i / 3 + j / 3 * 3][num] = 1;
                }
            }
        backTrack(board, 0, 0);
    }
private:
    int cols[9][9]{};
    int rows[9][9]{};
    int blocks[9][9]{};
    bool backTrack(vector<vector<char>>& board, int i, int j)
    {
        if(j == 9)
            return backTrack(board, i + 1, 0);
        if(i == 9)
            return true;
        if(board[i][j] != '.')
            return backTrack(board, i, j + 1);
        for(int k = 1; k <= 9; ++k)
        {
            if(cols[j][k - 1] || rows[i][k - 1] || blocks[i / 3 + j / 3 * 3][k - 1])
                continue;
            board[i][j] = k + '0';
            cols[j][k - 1] = 1;
            rows[i][k - 1] = 1;
            blocks[i / 3 + j / 3 * 3][k - 1] = 1;
            if(backTrack(board, i, j + 1))
                return true;
            board[i][j] = '.';
            cols[j][k - 1] = 0;
            rows[i][k - 1] = 0;
            blocks[i / 3 + j / 3 * 3][k - 1] = 0;
        }
        // 当所有填法都不行时，说明这种出问题了，就得回溯取消上面的步骤
        return false;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.3k Reading time ≈ 1 mins.

78. Subsets

backTrack

摘自wiki: 回溯法采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现，现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案

原
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> ret;
        ret.push_back({});
        vector<int> temp;
        for(size_t i = 1; i <= nums.size(); ++i)
            backTrack(ret, temp, nums, i, 0);
        return ret;
    }
private:
    void backTrack(vector<vector<int>>& ret, vector<int>& temp, vector<int>& nums, int n, int start)
    {
        if(temp.size() == n)
            ret.push_back(temp);
        if(temp.size() > n)
            return;
        for(size_t i = start; i < nums.size(); ++i)
        {
            temp.push_back(nums[i]);
            backTrack(ret, temp, nums, n, i + 1);
            temp.pop_back();
        }
    }
};
改
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> ret;
        vector<int> temp;
        backTrack(ret, temp, nums, 0);
        return ret;
    }
private:
    void backTrack(vector<vector<int>>& ret, vector<int>& temp, vector<int>& nums, int start)
    {
        ret.push_back(temp);
        for(size_t i = start; i < nums.size(); ++i)
        {
            temp.push_back(nums[i]);
            backTrack(ret, temp, nums, i + 1);
            temp.pop_back();
        }
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.7k Reading time ≈ 2 mins.

100. Same Tree

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if((p && !q) || (!p && q))
        {
            return false;
        }else if(!p && !p)
        {
            return true;
        }else if(p->val == q->val)
        {
            return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
        }
        return false;
    }
};

T(n) : O(N) S(n) : O(logN) 当平衡时，O(N) 当不平衡时，空间为递归所用的stack的大小

review
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(!p)
            return !q;
        if(!q)
            return !p;
        return p->val == q->val && isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 813 Reading time ≈ 1 mins.

40. Combination Sum II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<vector<int>> ret;
        sort(candidates.begin(), candidates.end());
        vector<int> temp;
        backTrack(ret, candidates, temp, target, 0);
        return ret;
    }
private:
    void backTrack(vector<vector<int>>& ret,vector<int>& candidates, vector<int>& temp, int remain, int start)
    {
        if(remain < 0)
            return;
        if(remain == 0)
        {
            ret.push_back(temp);
            return;
        }
        for(size_t i = start; i < candidates.size(); ++i)
        {
            temp.push_back(candidates[i]);
            backTrack(ret, candidates, temp, remain - candidates[i], i + 1);
            temp.pop_back();
            while(i+1 < candidates.size() && candidates[i] == candidates[i+1])
                ++i;
        }
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 811 Reading time ≈ 1 mins.

39. Combination Sum

backTrack

摘自wiki: 回溯法采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现，现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>> ret;
        vector<int> temp;
        backTrack(ret, candidates, temp, target, 0);
        return ret;
    }
private:
    void backTrack(vector<vector<int>>& ret, vector<int>& candidates, vector<int>& temp, int remain, int start) 
    {
        if(remain < 0)
            return;
        if(remain == 0) 
        {
            ret.push_back(temp);
            return;
        }
        for(size_t i = start; i < candidates.size(); ++i)
        {
            temp.push_back(candidates[i]);
            backTrack(ret, candidates, temp, remain - candidates[i], i);
            temp.pop_back();
        }
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 1.6k Reading time ≈ 1 mins.

36. Valid Sudoku

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        auto sz = board.size();
        int row[9][9]{0};
        int col[9][9]{0};
        int block[3][3][9]{0};
        for(size_t i = 0; i < 9; ++i)
        {
            for(size_t j = 0; j < 9; ++j)
            {
                auto num = board[i][j];
                if(num != '.')
                {
                    if(row[i][num - 49] == 1)
                        return false;
                    else
                        row[i][num - 49] += 1;
                    
                    if(col[num - 49][j] == 1)
                        return false;
                    else
                        col[num - 49][j] += 1;

                    if(block[i / 3][j / 3][num - 49] == 1)
                        return false;
                    else
                        block[i / 3][j / 3][num - 49] += 1;
                }
            }
        }
        return true;
    }
};

T : O(1) S : O(1)

more
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        auto sz = board.size();
        int row[9][9]{0};
        int col[9][9]{0};
        int block[3][3][9]{0};
        for(size_t i = 0; i < 9; ++i)
        {
            for(size_t j = 0; j < 9; ++j)
            {
                auto num = board[i][j];
                if(num != '.')
                {
                    if(row[i][num - 49] || col[num - 49][j] || block[i / 3][j / 3][num - 49])
                        return false;
                    else
                        row[i][num - 49] = col[num - 49][j] = block[i / 3][j / 3][num - 49] =  1;
                }
            }
        }
        return true;
    }
};
review
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        int row[9][9]{};
        int col[9][9]{};
        int square[9][9]{};
        for(int i = 0; i < 9; ++i)
        {
            for(int j = 0; j < 9; ++j)
            {
                if(board[i][j] == '.')
                    continue;
                int num = board[i][j] - '0' - 1;
                if(row[i][num] || col[j][num] || square[i / 3 + j / 3 * 3][num])
                    return false;
                row[i][num] = 1;
                col[j][num] = 1;
                square[i / 3 + j / 3 * 3][num] = 1;
            }
        }
        return true;
    }
};

Posted on Edited on In Disqus:
Symbols count in article: 318 Reading time ≈ 1 mins.

35. Search Insert Position

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        size_t lo = 0, hi = nums.size();
        while(lo < hi)
        {
            size_t mid = (lo + hi) / 2;
            if(nums[mid] < target)
            {
                lo = mid + 1;
            }else
            {
                hi = mid;
            }
        }
        return hi;
    }
};

T(n) : O(logN)
S(n) : O(1)

Posted on Edited on In Disqus:
Symbols count in article: 6.9k Reading time ≈ 6 mins.

23. Merge k Sorted Lists

Solution 1

思路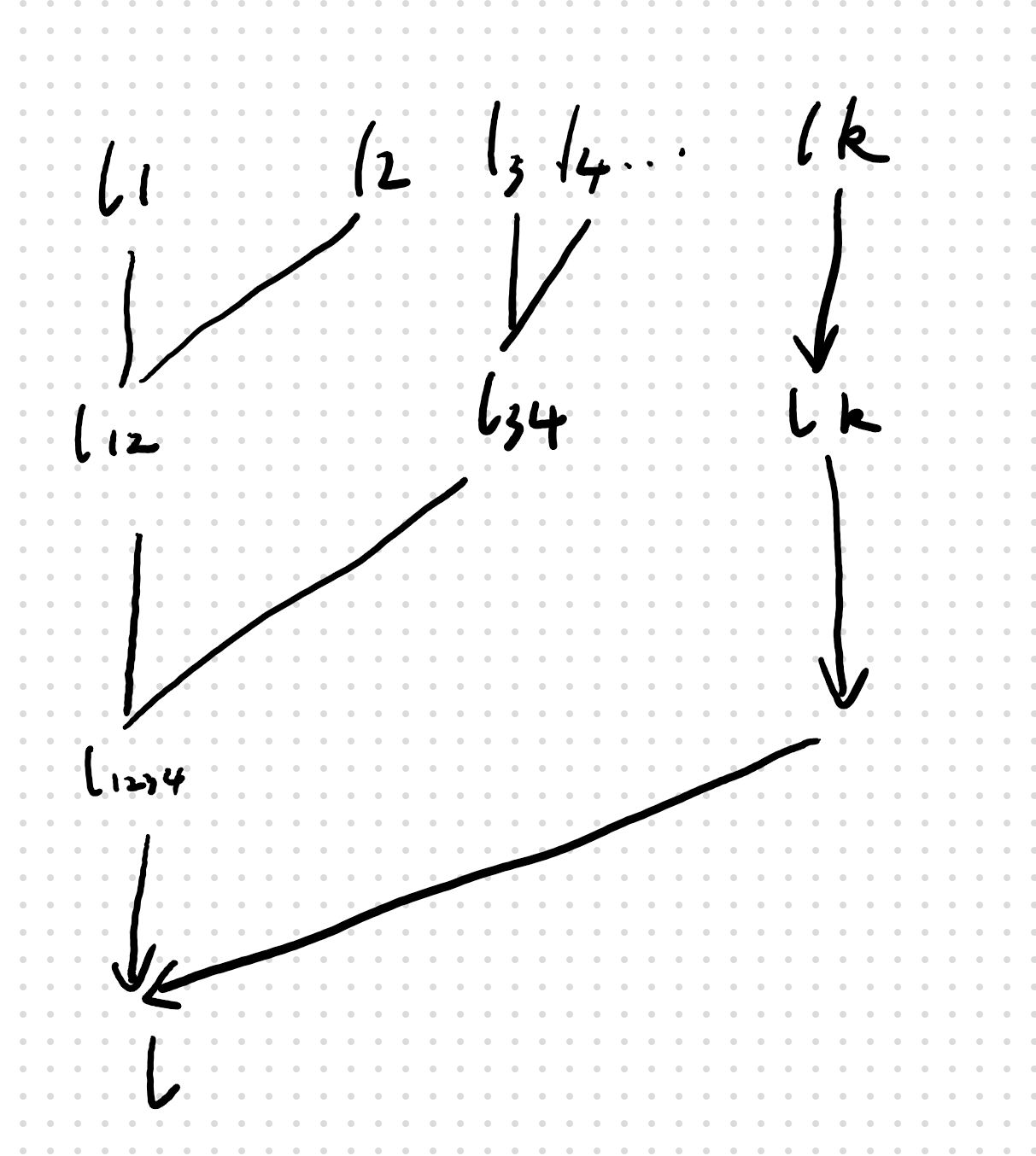 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if(lists.empty()) return nullptr;
        vector<ListNode*> newLists;   
        for(size_t i = 0; i < lists.size(); i = i + 2)
        {
            if(i != lists.size() - 1)
            {
                newLists.push_back(mergeTwoLists(lists[i], lists[i + 1]));
            }else
            {
                newLists.push_back(lists[i]);
            }
        }
        if(newLists.size() == 1)
            return newLists[0];
        
        return mergeKLists(newLists);
    }
private:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2)
    {
        if(!l1) return l2;
        if(!l2) return l1;
        while(l1 && l2)
        {
            if(l1->val > l2->val)
            {
                l2->next = mergeTwoLists(l1, l2->next);
                return l2;
            }else
            {
                l1->next = mergeTwoLists(l1->next, l2);
                return l1;
            }
        }
        return nullptr;
    }
};
Time complexity: O(NlogK)
Space complexity: O(logK)

优化后 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        int stride = 1;
        int sz = lists.size();
        while(stride < sz)
        {
            for(size_t i = 0; i < sz - stride; i = i + 2 * stride)
            {
                lists[i] = mergeTwoLists(lists[i], lists[i + stride]);
            }
            stride *= 2;
        }   
        return lists.empty() ? nullptr : lists[0];
    }
private:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2)
    {
        if(!l1) return l2;
        if(!l2) return l1;
        while(l1 && l2)
        {
            if(l1->val > l2->val)
            {
                l2->next = mergeTwoLists(l1, l2->next);
                return l2;
            }else
            {
                l1->next = mergeTwoLists(l1->next, l2);
                return l1;
            }
        }
        return nullptr;
    }
};
Time complexity: O(NlogK)
Space complexity: O(1)

review
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        for(int step = 1; step < lists.size(); step *= 2)
        {
            for(int i = 0; i < lists.size() - step; i += 2 * step)
                lists[i] = merge(lists[i], lists[i + step]);
        }
        return lists.empty() ? nullptr : lists[0];
    }
private:
    ListNode* merge(ListNode* l1, ListNode* l2)
    {
        if(!l1)
            return l2;
        if(!l2)
            return l1;
        
        if(l1->val > l2->val)
        {
            l2->next = merge(l1, l2->next);
            return l2;
        }else
        {
            l1->next = merge(l1->next, l2);
            return l1;
        }
        return nullptr;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if(lists.empty())
            return nullptr;
        int n = lists.size();
        for(int stride = 1; stride < n; stride *= 2)  // 这里是为了可以是最前面和最后面归并，如果是奇数，会最后第一个和最后一个一起归，如果是偶数，那就不用了
        {
            for(int i = 0; i < n - stride; i += stride * 2) // (注意这个n-stride十分重要，因为最后一步中i的位置是位于n-sride-1,所以需要让i停下来)(可能并不重要？因为我后面不用也可以)我后面不用是因为我进行了判断
                lists[i] = merge(lists[i], lists[i + stride]);
        }
        return lists[0];
    }
private:
    ListNode* merge(ListNode* l1, ListNode* l2)
    {
        ListNode ret;
        ListNode* pseudoHead = &ret;
        while(l2 && l1)
        {
            if(l1->val < l2->val)
            {
                pseudoHead->next = l1;
                l1 = l1->next;
            }
            else
            {
                pseudoHead->next = l2;
                l2 = l2->next;
            }
            pseudoHead = pseudoHead->next;
        }
        pseudoHead->next = l1 ? l1 : l2;
        return ret.next;
    }
};
再次review
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if(lists.empty())
            return nullptr;
        int n = lists.size();
        for(int step = 1; step < n; step *= 2)
            for(int i = 0; i < n; i += step * 2)
                lists[i] = merge(lists[i], i + step < n ? lists[i + step] : nullptr); //这里我进行了判断，所以不用担心超出了范围
        return lists[0];
    }
private:
    ListNode* merge(ListNode* l1, ListNode* l2)
    {
        if(!l1)
            return l2;
        if(!l2)
            return l1;
        if(l1->val < l2->val)
        {
            l1->next = merge(l1->next, l2);
            return l1;
        }else
        {
            l2->next = merge(l2->next, l1);
            return l2;
        }
        return nullptr;
    }
};
Solution 2 use priority_queue
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class cuscomp
{
public:
    bool operator()(pair<int, ListNode *> p1, pair<int, ListNode *> p2)
    {
        return p1.first > p2.first;
    }
};
class Solution
{
public:
    ListNode *mergeKLists(vector<ListNode *> &lists)
    {
        std::priority_queue<pair<int, ListNode *>, std::vector<pair<int, ListNode *>>, cuscomp> q;
        ListNode *point = new ListNode();
        ListNode *head = point;
        for (auto &list : lists)
        {
            if(list)
                q.push(make_pair(list->val, list));
        }
        while (!q.empty())
        {
            auto node = q.top().second;
            q.pop();
            point->next = new ListNode(node->val);
            point = point->next;
            node = node->next;
            if (node)
                q.push(make_pair(node->val, node));
        }
        return head->next;
    }
};
review
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        priority_queue<ListNode*, vector<ListNode*>, cusComp> pq;
        ListNode* pesudoHead = new ListNode();
        ListNode* point = pesudoHead;
        for(auto& node : lists)
            if(node)
                pq.push(node);
        while(!pq.empty())
        {
            auto p = pq.top();
            pq.pop();
            point->next = p;
            point = point->next;
            if(p->next)
                pq.push(p->next);
        }
        return pesudoHead->next;
    }
private:
    class cusComp
    {
    public:
        bool operator()(ListNode* p1, ListNode* p2)
        {
            return p1->val > p2->val;
        }
    };
};

Time complexity: O(NlogK)
Space complexity: O(N)