Cinte's Leetcode Record
0%

55. Jump Game

Posted on Edited on In Disqus:
Symbols count in article: 2.2k Reading time ≈ 2 mins.

55. Jump Game

这段话很好

跟着答案走

动态规划

首先，确定网格中最后一个元素可以到达他本身，自上而下，进行判断前一个可以到达他的元素是什么
由此，慢慢的，从后面开始，可以到达最后一块的坐标都被用good填充，这样一来，其他的回溯只需要判断能否到达这些good的点即可，而无需全都走到最后一个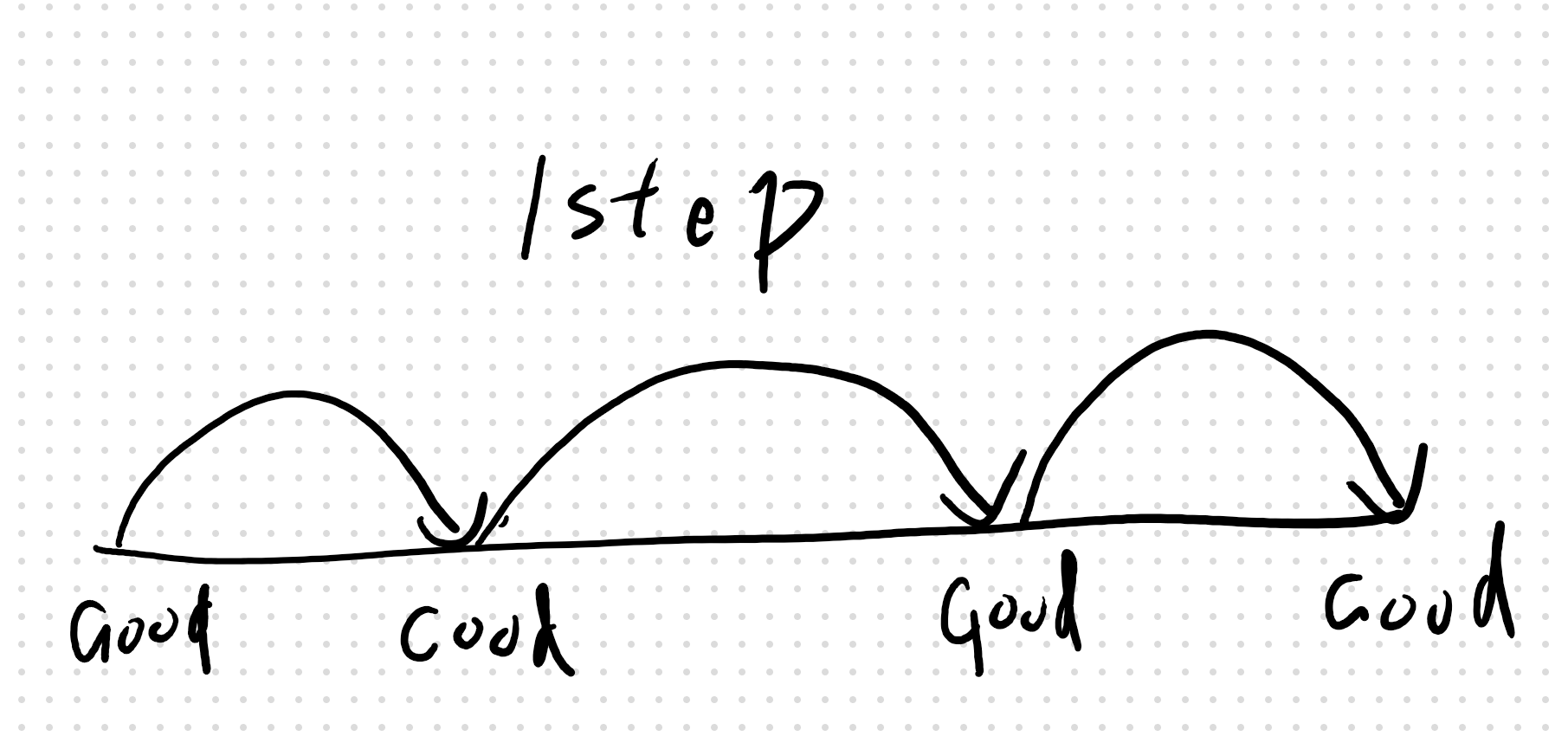 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
enum status {
    GOOD,
    BAD,
    UNKNOW
};
class Solution {
public:
    bool canJump(vector<int>& nums) {
        dp = new status[nums.size()];
        fill(dp, dp + nums.size(), UNKNOW);
        dp[nums.size() - 1] = GOOD;
        return backTrack(nums, 0);
    }
private:
    status* dp;
    bool backTrack(vector<int>& nums, int start)
    {
        if(dp[start] != UNKNOW)
            return dp[start] == GOOD;
        
        int maxPos = (start + nums[start] > nums.size() - 1) ? nums.size() - 1 : start + nums[start];
        
        for(int pos = start + 1; pos <= maxPos; ++pos)
        {
            if(backTrack(nums, pos))
            {
                dp[start] = GOOD;
                return true;
            }
        }
        dp[start] = BAD;
        return false;
    }
};
T(n) : O(n^2)
S(n) : O(n)

bottom Up

从最后出发，判断前一步可不可以走到一个good，依次回去。 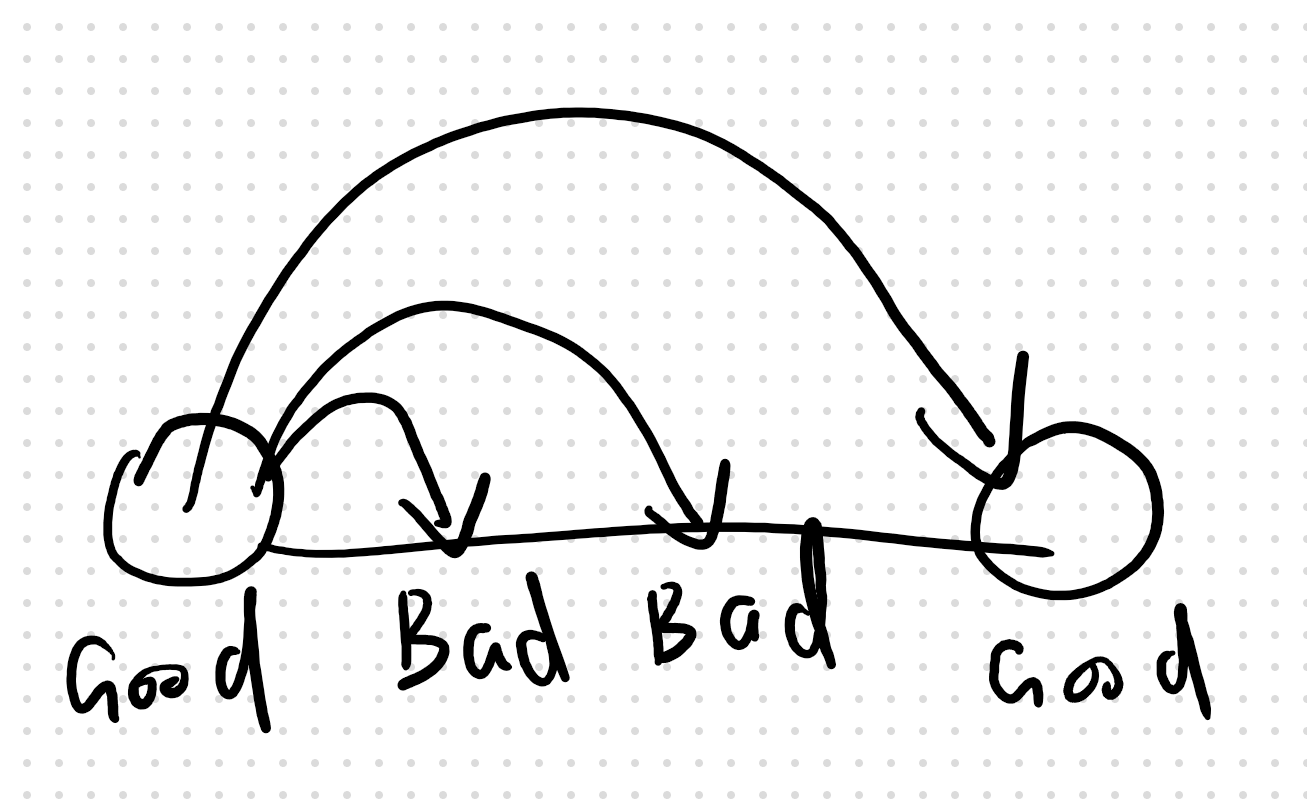image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
enum status
{
    UNKNOW,
    GOOD
};
class Solution {
public:
    bool canJump(vector<int>& nums) {
        status* dp = new status[nums.size()];
        fill(dp, dp + nums.size(), UNKNOW);
        dp[nums.size() - 1] = GOOD;
        for(int pos = nums.size() - 2; pos >= 0; --pos)
        {
            int maxPos = pos + nums[pos] > nums.size() - 1 ? nums.size() - 1 : pos + nums[pos];
            for(int cur = maxPos; cur > pos; --cur)
            {
                if(dp[cur] == GOOD)
                {
                    dp[pos] = GOOD;
                    break;
                }
            }
        }
        return dp[0] == GOOD;
    }
};

T(n) : O(n^2)
S(n) : O(n)

greedy

对于一路上的所有good，我能走到右边的就能走到左边的一个good，因此 只需要记录最左边的一个的坐标，空间复杂度降为O(1)

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    bool canJump(vector<int>& nums) {
        int lastPos = nums.size() - 1;
        for(int pos = nums.size() - 2; pos >=0 ; --pos)
        {
            if(pos + nums[pos] >= lastPos)
                lastPos = pos;
        }
        return lastPos == 0;
    }
};

T(n) : O(n)
S(n) : O(1)

更greedy
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool canJump(vector<int>& nums) {
        int maxReach = 0;
        int i = 0;
        for(i; i < nums.size() && maxReach >= i; ++i)
        {
            maxReach = max(i + nums[i], maxReach);
            if(maxReach >= nums.size() - 1) return true;
        }
        return maxReach >= nums.size() - 1;
    }
};

每步都贪，贪不了了就停了

review 

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool canJump(vector<int>& nums) {
        int farest = 0;
        for(int i = 0, sz = nums.size(); i < sz; ++i)
        {
            if(farest < i)
                return false;
            farest = max(farest, i + nums[i]);
        }
        return true;
    }
};